Convex set은 집합의 두 점을 선으로 연결했을 때 해당 선 위의 모든 점들이 해당 집합에 포함되는 집합으로, convex optimization의 기본이 되는 개념이다. 최적화 문제를 convex function으로 변환함으로써 gradient descent 등의 방법을 통해 쉽게 해결할 수 있기 때문에, convex set은 loss를 minimize하는 것을 목적으로 하는 딥러닝을 공부하기 위해서 중요한 개념이라고 할 수 있다. 이번 글에서는 convex set이 무엇인지와 함께, convex set을 포함하는 개념인 affine set이 무엇인지에 대해서도 알아보겠다.
Affine set
Affine set이 무엇인지에 대해 알아보기 전에, affine combination이 무엇인지에 대해 먼저 알아보겠다. Affine combination은 다음과 같이 정의할 수 있다.

예를 들어, $x_1=(0,1)$, $x_2=(1,0)$이라고 하자. 그럼 이 두 점의 모든 affine combination은 다음과 같이, $(1,0)$과 $(0,1)$을 지나는 직선 형태로 표현할 수 있을 것이다. 즉, affine combination은 점들 간의 직선 위에 항상 위치한다.
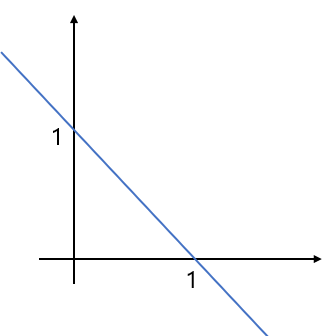
다음으로, affine set은 다음과 같이 정의할 수 있다. 두 점 $x_1$, $x_2$가 집합 $C$ 안에 속해 있을 때, 두 점을 잇는 직선 위에 있는 모든 점이 집합 $C$ 안에 항상 포함된다면, 이 집합 $C$는 affine set이라고 할 수 있는 것이다.

마지막으로, affine hull은 어떤 집합 $C$의 모든 affine combination의 집합을 말한다. 이는 다음과 같이 정의할 수 있다.

Convex set
Convex set은 affine set에서 모든 $\theta$ 조건을 양수로 바꾸면 된다. 그러므로 affine combination이 두 점을 지나는 직선 형태로 표현되었다면, convex combination은 두 점을 지나는 선분 형태로, affine set이 두 점을 지나는 직선이 모두 포함된 집합을 표현했다면 convex set은 두 점을 지나는 선분이 모두 포함된 집합을 표현한다. Convex combination은 다음과 같이 정의할 수 있다.

예를 들어, $x_1=(0,1)$, $x_2=(1,0)$이라고 하자. 그럼 이 두 점의 모든 affine combination은 다음과 같이, $(1,0)$과 $(0,1)$을 지나는 선분 형태로 표현할 수 있을 것이다. 즉, convex combination은 점들 간의 선분 위에 항상 위치한다.

다음으로, convex set은 다음과 같이 정의할 수 있다. 두 점 $x_1$, $x_2$가 집합 $C$ 안에 속해 있을 때, 두 점을 잇는 선분 위에 있는 모든 점이 집합 $C$ 안에 항상 포함된다면, 이 집합 $C$는 convex set이라고 할 수 있는 것이다.

예를 들어, 다음과 같은 두 개의 회색 집합이 있다고 하자.

왼쪽의 집합은 집합 내의 어떤 점을 선택하든 연결하는 선분이 해당 집합 안에 포함되기 때문에 convex set이라고 할 수 있다. 이에 반해, 오른쪽 집합은 위 그림과 같이 $x_1$과 $x_2$를 선택하면 선분의 가운데 부분이 집합에 포함되지 않기 때문에 convex하지 않은 set이다.
마지막으로, convex hull은 어떤 집합 $C$의 모든 convex combination의 집합을 말하고, 다음과 같이 정의할 수 있다. Convex hull은 항상 convex set이고, 집합 $C$를 포함하는 가장 작은 convex set이다.

위에서 살펴보았던 예시 non convex set의 convex hull은 아래 그림과 같다.

이번 글에서는 convex set과 affine set이 무엇인지와 함께, 이에 연관된 개념들인 convex/affine combination과 hull에 대해서 알아보았다. 이 글에 이어서 convex function과 함께, 간단한 convex optimzation에 대한 글도 써보겠다.








최근댓글