ODE는 ordinary differential equation의 준말로, 어떤 variable과 그것의 미분으로 구성된 방정식을 말한다. 그리고 SDE는 stochastic differential equation의 준말로, 하나 이상의 term이 stochastic process인 미분방정식, 즉 randomness를 가지는 부분이 있는 미분방정식을 말한다. 이번 글에서는 ODE와 SDE가 무엇인지에 대해, 수학자의 관점 보다는 diffusion model과 score-based generative model을 이해하기 위한 관점으로 알아보겠다.
ODE
ODE는 어떤 variable과 그것의 미분으로 구성된 방정식을 말하고, 이것의 기본적인 형태는 다음과 같다.

위 식에서 $x(t)$는 시간 $t$일 때 함수 $x$의 값, $\frac{dx(t)}{dt}$는 $x(t)$가 $t$가 변함에 따라 변하는 비율을 의미한다고 해석할 수 있다. 즉, "ODE를 푼다"라는 것은 "위 식을 만족하는 함수들의 set을 찾는 것"이라고 할 수 있다. 위 형태와 같은 ODE는 다음과 같은 식을 통해서 solution을 구할 수 있다.
머신러닝에서 ODE를 사용하는 이점은 free parameter의 개수가 줄어들어 더 효율적인 연산을 할 수 있다는 것이다. 예를 들어, 우리가 어떤 x(t)와 t 값들이 주어졌을 때, 다음과 같은 식을 만족하는 regression 문제를 풀어야 한다고 하자.

이 식을 풀기 위해서 우리는 a와 b 두 개의 free parameter를 구해야 할 것이다. 하지만 ODE를 사용하면 다음과 같은 식을 풀면 된다. (initial data point 하나가 주어졌다고 가정한다.)

이 식을 풀기 위해 우리는 a 하나의 free parameter만 구하면 된다. 즉, 위에서 설명했듯이 위 식을 만족하는 함수들의 set을 찾음으로써 문제를 더 간소화하여 더 효율적인 연산을 할 수 있는 것이다.
SDE
SDE는 하나 이상의 term이 stochastic process인 미분방정식, 즉 randomness를 포함하고 있는 미분방정식을 말한다. Stochastic process는 시간 t에 따라 변하는 각 state들을 표현하는 process로, 이 시간에 따라 변하는 결과는 deterministic하지 않고 randomness를 가진다. 즉, 시간이 흐름에 따라 프로세스가 항상 같은 것이 아니라 randomness에 의해 조금씩 달라지는 것이다. SDE의 기본적인 형태는 다음과 같다.
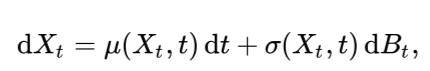
위 식에서 $\sigma(X_t, t)dB_t$ 부분이 없다면 이는 위에서 설명했던 ODE와 동일한 형태가 될 것이다. 하지만 randomness를 포함하는 $dB_t$가 포함됨으로써 이 식이 SDE가 되는 것이다. 위 식에서 첫 번째 term인 $\mu(X_t, t)$는 drift term이라고 불린다. 이 부분은 ODE와 마찬가지로 randomness 없이 detereministic한 부분이다. 두 번째 term인 $\sigma(X_t, t)dB_t$는 diffusion term이라고 불린다. $B_t$가 어떤 랜덤한 프로세스를 의미하고, 이러한 랜덤한 프로세스가 전체 프로세스에 얼마나 영향을 미치는지를 표현하는 부분이다. 이 랜덤한 프로세스는 주로 Wiener process로 정의되는데, 쉽게 말해 가장 일반적으로 표현되는 랜덤한 프로세스, 즉 noise의 식이라고 이해하면 된다.
이번 글에서는 SDE와 ODE가 무엇인지에 대해 알아보았다. 이번 글을 시작으로 추가적인 SDE에 관련된 개념들과 함께 diffusion model과 SDE가 어떻게 연관되는지까지 알아보겠다.








최근댓글