Langevin dynamics는 복잡한 시스템에서 입자들의 움직임을 시뮬레이션하기 위한 방법으로, score function을 기반으로 하는 SDE를 활용하는 diffusion model에서 샘플링을 하는 방법으로 널리 사용된다. 이번 글에서는 이러한 Langevin dynamics가 어떻게 유도되고, generative model에서 어떻게 사용되는지에 대해 알아보겠다.
Fokker-Planck equation
Fokker-Planck equation은 probability density function이 시간이 흐르면서 stochastic process를 거쳐 어떻게 변하는지를 표현하는 미분방정식이다. 확률 분포는 시간이 흐르면서 어떠한 stationary distribution, 즉 더 이상 확률 분포가 변하지 않는 지점에 도달하기도 한다.우리가 Fokker-Planck equation에 대해 알아야 하는 이유는, 결국 SDE를 활용하여 generative model을 모델링 할 때의 목적이 최종적인 stationary distribution이 우리가 목적으로 하는 data distribution을 따르는 SDE를 찾는 것이기 때문이다.
기본적인 SDE가 아래 식과 같이 어떤 하나의 샘플이 시간이 흐르면서 어떻게 변하는지를 표현하는 individual sample path를 표현했다면, Fokker-Planck equation은 하나의 샘플이 아닌 probability distribution 전체가 시간이 흐르면서 어떻게 변하는지를 표현하기 때문에 더 넓은 범위를 다루고 있다고 할 수 있다. 즉, SDE에 대한 해들의 확률 분포가 Fokker-Planck equation의 해가 된다.

Fokker-Planck equation은 다음과 같은 식으로 표현된다. 아래 식에서 $p_s(\mathbf{x}(t);t)$는 어떤 확률 분포를 의미하고, generative model의 목적은 이 확률 분포의 stationary distribution이 data distribution으로 수렴하는 적절한 f와 g를 찾는 것이다.

Stationary distribution의 정의는 다음과 같이 어떤 단위 시간 동안 확률 분포의 변화량이 0인 것, 즉 미분 값이 0인 분포이다.

이 식을 가만히 살펴 보면 Fokker-Planck equation의 왼쪽 항과 같은 것을 알 수 있다. 그러므로 stationary distribution은 다음과 같은 식을 만족할 것이다.
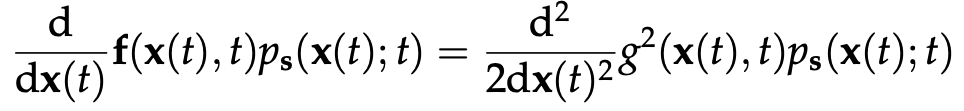
이 식을 만족하는 stationary distribution p를 찾기 위해서는 굉장히 복잡한 계산이 필요할 것이다. 하지만 f와 g를 적절하게 잘 정의한다면, 그 계산이 좀 더 쉬워질 수 있다.
Langevin dynamics
Langevin equation은 다음과 같은 식이다. 아래 식에서 w(t)는 Wiener process를 의미한다.

이제 우리가 이 Langevin equation을 통해서 어떻게 stationary distribution을 얻어낼 수 있는지에 대해 알아보겠다. 쉬운 stationary distribution의 계산을 위해 f와 g를 각각 다음과 같은 식으로 표현한다고 하자.
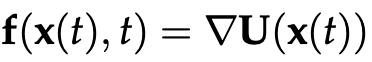

그러면 우리는 다음과 같은 깔끔한 형태의 stationary distribution을 얻을 수 있다.

이 식을 통해 우리는 x(t)가 U(x(t))의 exponential에 비례하여, 즉 Boltzmann distribution을 따르면서 샘플링이 될 것이라는 것을 알 수 있다.
Stationary distribution 증명 (생략 가능)
위 식이 Fokker-Planck equation을 활용한 stationary distribution의 조건을 만족하는지에 대한 의구심이 들 수 있다. 이에 대한 확인을 위해 위에서 주어진 f, g 그리고 stationary distribution을 대입하면 다음과 같다.

위 식의 오른쪽 항을 한 번 미분하면 다음과 같이 등식이 성립하는 것을 알 수 있다.

Sampling from Langevin dynamics
이제 이 Langevin equation을 활용해서 어떻게 샘플링을 할 수 있는지에 대해 알아보겠다. 우리가 $\Delta U(x(t))$ 대신에 probability distribution의 미분, 즉 score function에서 2를 나눈 값을 대입하고, k를 1로 놓는다고 하자. 그러면 우리는 다음과 같은 Langevin equation을 얻을 수 있다.
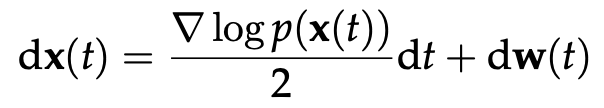
이러한 특별한 형태의 Langevin equation의 장점은, 우리가 data distribution을 안다는 가정 하에 stationary distribution이 data distribution과 같도록 만들 수 있다는 것이다. 즉, 우리의 원래의 목적이었던 최종적인 stationary distribution이 우리가 목적으로 하는 data distribution을 따르는 SDE를 찾는 것을 달성할 수 있게 된다.

달리 말해, 우리가 probability distribution의 미분 값인 score function만 잘 추정한다면 true data distribution을 따르는 샘플을 잘 만들어 내는 generative model을 만들 수 있게 되는 것이다. 이러한 이유로 score function을 활용한 diffusion model 방법들이 다양하게 등장하기 시작한 것이다. 이러한 Langevin equation으로부터 샘플링을 할 때에는 다양한 방법을 적용할 수 있지만, 가장 간단하게는 다음과 같이 Euler-Maruyama method를 적용시킬 수 있다.
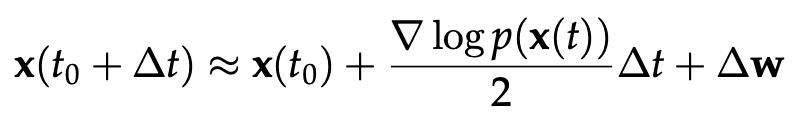
즉, Wiener process의 delta 값($\Delta w$)을 하나 샘플링하고, 그것을 활용해서 다음 x 값을 update하는 과정을 반복함으로써 true data distribution을 따르는 샘플링이 가능해진다.

이번 글에서는 Langevin dynamics가 무엇이고, 이것으로부터 샘플링을 어떻게 진행하며 이것이 왜 diffusion model과 연관되어 있는지에 대해 알아보았다. 다음 글부터는 본격적으로 diffusion model의 기본적인 논문들을 다루어보겠다.








최근댓글