Trace Clustering이란, 프로세스 마이닝에서 비슷한 속성을 가진 trace들을 clustering하는 것을 말한다. process discovery 전의 trace clustering은 비교적 보기 쉽고 간단한 모델을 도출하는 데에 큰 도움을 준다.
2019/11/23 - [Process Mining & Data Mining] - 프로세스 마이닝의 trace clustering
프로세스 마이닝의 trace clustering
간만의 포스팅. 블로그 시작한 이후로 가장 긴 공백기였던 것 같다. 다른 것을 쓰고 있어서 집에서까지 글을 쓰고 싶지 않았다 ㅎㅎ 실제 이벤트 로그는 크고 복잡하다. 그래서 이 이벤트 로그로 프로세스 모델을..
process-mining.tistory.com
하지만 보통의 trace clustering 방법은 해당 액티비티의 앞뒤에 어떤 액티비티가 일어났는지(context)나 액티비티가 일어난 순서(order) 등은 고려하지 못한다는 한계점을 가진다. 이번 포스팅에서는 이러한 한계점을 극복하기 위해 제시된 trace clustering 방법인 Context Aware Trace Clustering에 대해 알아보겠다.
기본 개념
기본적으로 trace clustering에서 사용되는 개념에는 substitution, insertion, deletion이 있다.
- substitution: 서로 다른 두 액티비티가 같은 자리에서 일어나는 경우를 말한다. 예를 들어, S = <a, b, c>, T = <a, b, d>라는 두 trace가 있으면 S(3)이 c, T(3)이 d이므로 둘은 substitution이다.
- insertion: 한 trace에는 존재하나 다른 trace에는 존재하지 않아 삽입해주어야 하는 경우를 말한다. 예를 들어, S = <a, b, c>, T = <a, c>일 때 T에 b가 insertion되어야 같아진다.
- deletion: insertion의 반대 개념이다. 위에서와 같은 예로 S = <a, b, c>, T = <a, c>일 때 S에서 b가 deletion되어야 같아진다.
trace의 clustering을 위해서는 비슷한 trace끼리 묶어야 하기 때문에 각 trace가 얼마나 비슷한지, 즉 trace 간의 similarity를 계산할 수 있어야 한다. 이를 위해서 기본적으로 지켜져야 하는 원칙은 다음과 같다.
- uncorrelated activity들 간의 substitution은 두 trace의 similarity를 낮춘다.
- contrast activity들 간의 substitution은 두 trace의 similarity를 많이 낮춘다.
- context 밖의 (서로 짧은 시간 안에 같이 일어나지 않은) activity의 insertion은 두 trace의 similariity를 낮춘다.
- correlatied/similar activity의 substitution은 두 trace의 simlarity를 높인다.
이 기본 원칙과 함께, 각 액티비티 간의 substitution score와 indel score를 계산함으로써 trace 간의 simliarity를 계산할 수 있다.
Substitution Score
Subtitution score를 계산하는 알고리즘은 다음과 같다.

이를 예시와 함께 한 단계 한 단계 친절하게 설명해보도록 하겠다. 우선, 우리의 이벤트 로그는 다음과 같다. 우리는 액티비티 a와 b의 substitution score를 구할 것이다.
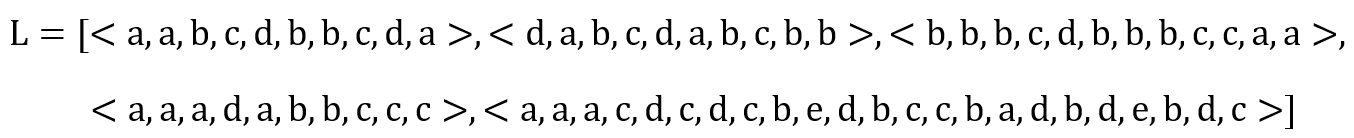
1. 우선, 이벤트 로그에 대해 모든 3-gram set과 각 element의 빈도를 구한다.
3-gram set이란 이벤트 로그에서 찾을 수 있는 모든 3개의 연속한 액티비티 sequence를 뜻한다. 예를 들어, <a, b, c, d, a>라는 trace가 있으면 이것의 3-gram set은 {abc, bcd, cda}가 된다. 우리의 예시 이벤트 로그 L에서 3-gram set을 찾으면 다음과 같다.

그리고 이 각 3-gram element들의 이벤트 로그 내에서의 빈도를 구하면 다음과 같다.

2. 다음으로, 각 activity의 context set을 구한다.
context set이란, 해당 액티비티의 앞뒤로 있을 수 있는 액티비티 set을 말한다. 예를 들어, 3-gram set {abc, dbc, abd}가 있다고 하면 액티비티 b의 context set은 {ac, dc, ad}가 되는 것이다. 이를 우리의 예시 이벤트 로그에 적용시켜 액티비티 a와 b의 context set을 구하면 다음과 같다.

3. 두 액티비티의 context set 중 교집합을 구한다.

4. 3의 각 원소에 대해 co-occurrence combination을 구한다.
co-occurrence combination은 다음과 같이 설명할 수 있다. 예를 들어, 우리의 예시에서 db의 액티비티 a, b에 대한 co-occurrence combination을 구한다고 하자. 그러면 우리는 dab의 빈도(3) * dbb의 빈도(2)를 곱하여 6이라는 co-occurrence combination을 도출할 수 있다. 이를 식으로 표현하면 다음과 같다.

우리의 예시에 대해 co-occurrence combination을 구하면 각각 1, 2, 1, 6이 된다.

그리고 이를 모두 더해줌으로써 우리는 C(a, b)값도 구할 수 있다. 그러므로 우리의 C(a, b) 값은 10이 된다.
5. 모든 액티비티 pair에 대해 co-occurrence combination 값을 normalize한 행렬을 만들어준다.
모든 액티비티 pair에 대해 4의 과정을 통해 C(a, b) 값을 구할 수 있을 것이다. 이들을 모두 구하고, 이들을 모두 합한 값으로 나눈 값으로 이루어진 행렬 M(a, b)를 만들어준다.
6. 5에서 만든 행렬을 바탕으로 probability of occurrence 값을 구한다.
probability of occurrence 값은 다음 계산식에 따라 계산할 수 있다.

7. 6에서 구한 p 값을 바탕으로 expected value of occurrence 값을 구하고, 이를 바탕으로 substitution score를 구한다.
Expected value of occurrence는 다음과 같은 식으로 계산할 수 있다.
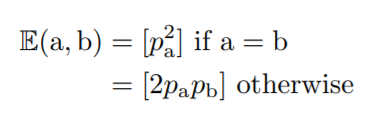
그리고 이를 바탕으로 하여, substitution score는 다음과 같이 계산할 수 있다.

위와 같은 긴 과정을 통해서 각 액티비티 간의 substitution score를 계산할 수 있다.
Indel Score
Indel score에는 insertionRightGivenLeft와 insertionLeftGivenRight의 두 가지 종류가 있다. insertionRightGivenLeft(a/b)는 액티비티 a를 b의 오른쪽(right)에 넣는 것을 말한다. 이와 반대로, insertionLeftGivenRight(a/b)는 액티비티 a를 b의 왼쪽(left)에 넣는 것을 말한다. 이를 구하는 알고리즘은 다음과 같다.

이를 다시 위에서 쓴 것과 같은 예시와 함께 풀어 써 보겠다.
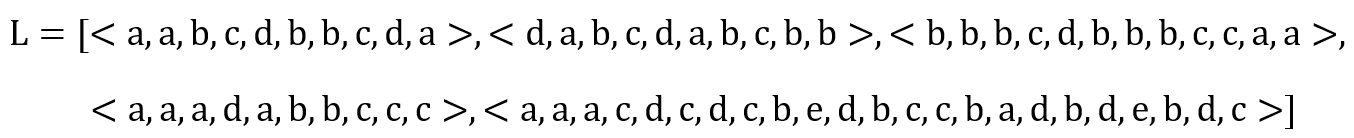
1. substitution score를 구할 때 사용했던 3-gram set과 이의 빈도를 구한다.
위에서 이는 설명했기 때문에 결과값만 제시하고 넘어가도록 하겠다.

그리고 이 각 3-gram element들의 이벤트 로그 내에서의 빈도를 구하면 다음과 같다.

2. 다음으로, 각 activity의 context set을 구한다.
이도 위에서 설명했기 때문에 넘어가도록 하겠다.

3. 각 액티비티의 context set에 대해서 각 3-gram이 일어난 빈도를 구한다.
예를 들어, C_xy(a)는 xay가 이벤트 로그 내에서 일어난 빈도이다. 이 빈도를 모든 context set에 대해서 구해준다.
4. 각 액티비티 set에 대해 countRightGivenLeft(a/x) 값을 구해준다.
countRightGivenLeft(a/x) 값은 다음과 같이 정의할 수 있다.

즉, context set에서 뒷 액티비티가 같은 것끼리 C 값을 모두 더해주는 것이다. 예를 들어, 우리가 (a/a)의 countRightGivenLeft 값을 구하고 싶으면 다음과 같이 구할 수 있다.

5. 모든 액티비티에 대해 countRightGivenLeft 값을 normalize해준다.
모든 액티비티에 대해 countRightGivenLeft(a/x) 값을 구할 수 있을 것이다. 이들을 모두 더한 값으로 나누어준 값인 normCountRightGivenLeft(a/b) 값을 구한다.


6. 모든 액티비티에 대해 각 액티비티의 일어날 확률 값인 p_a 값을 구해준다.
7. 다음 식을 통해 indel score 값을 구한다.

위와 같은 긴 과정을 통해서 각 액티비티 간의 indel score를 계산할 수 있다.
Trace 간 similarity 계산
이제 위의 긴 과정을 통해 구한 각 액티비티 간의 substitution score와 indel score 값을 이용하여 trace 간의 similarity 값을 계산할 차례이다. 이는 다음과 같은 식을 통해서 계산할 수 있다.

위 식에서 S^m, T^n은 각각 m과 n의 길이를 가지는 trace, S(m)은 S trace의 m번째 자리 액티비티, T(n)은 T trace의 n번째 자리 액티비티, s(S(m), T(n))은 substitution score, i(S(m), -)과 i(-, T(n))은 indel score를 의미한다. 이렇게 simliarity를 정의하고 나면 우리는 각 trace 간의 distance도 계산할 수 있다.

이 distance를 기반으로 우리는 context를 고려한 trace clustering을 진행할 수 있다.
이번 포스팅에서는 저번 trace clustering 포스팅에서 한 단계 발전한, context aware trace clustering에 대해 다루었다.
References
R. P. Jagadeesh Chandra Bose and Wil M.P. van der Aalst, "Context Aware Trace Clustering: Towards Improving Process Mining Results", Proceedings of the 2009 SIAM International Conference on Data Mining. 2009, 401-412








최근댓글