제너럴한 데이터 마이닝 글이 조회수가 잘 나오는 걸 알지만 나는 쓴다 프로세스 마이닝. ㅎㅎ 저번 포스팅에서 우리는 페트리 넷(Petri Net)이 무엇인지에 대해 알아보았다. 논문들을 읽다 보면 페트리 넷이 P-net이라거나 Free-choice net이라고 가정을 하고 논리를 전개해나가는 경우가 꽤 있다. 이번 포스팅에서는, 페트리 넷의 종류들 중 P-net, T-net, Free-Choice Net에 대해 알아보겠다.
P-net (state machine)
P-net은 다른 말로 state machine이라고도 부른다. P-net은 다음과 같이 정의할 수 있다.

즉, 페트리 넷 내의 모든 트랜지션들의 input과 output flow가 하나인 페트리 넷을 말한다. 예를 들어, 다음과 같은 페트리 넷이 있다고 하자.
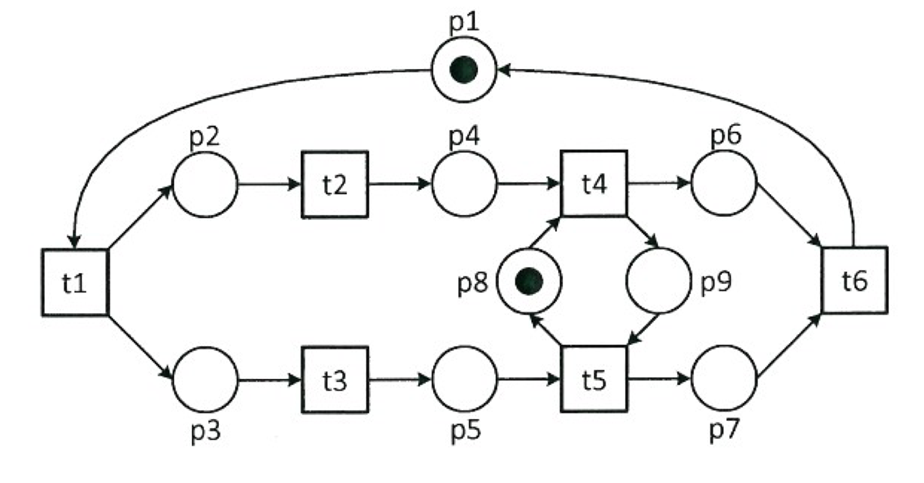
이 페트리 넷은 P-net이라고 할 수 있을까? 답은 아니다. t1의 output flow가 2개, t6의 input flow가 2개 등 1 초과인 트랜지션들이 존재하기 때문이다.
T-net (marked graph)
T-net은 다른 말로 marked graph라고도 부를 수 있다. T-net은 다음과 같이 정의할 수 있다.

즉, 페트리 넷 내의 모든 place들의 input과 output flow가 하나인 페트리 넷을 말한다. 또 위의 예시 페트리 넷을 살펴보자.

이 페트리 넷은 T-net이라고 할 수 있을까? 답은 맞다. 모든 place들에 대해서 input flow와 output flow가 하나씩밖에 없기 때문이다.
Free-choice net
Free-choice net은 다음과 같이 정의할 수 있다.

즉, 모든 서로 다른 트랜지션들에 대해 트랜지션으로 들어가는 input place가 똑같거나 둘의 교집합이 아예 없는 페트리 넷을 말한다. 다시 위 예시 페트리 넷을 보자.

이 페트리 넷은 free-choice net일까? 답은 맞다. 모든 트랜지션들에 대해서 트랜지션의 input place가 교집합을 가지는 트랜지션이 존재하지 않는다. 하지만 만약 아래와 같은 페트리 넷이 있다면 어떻게 될까?
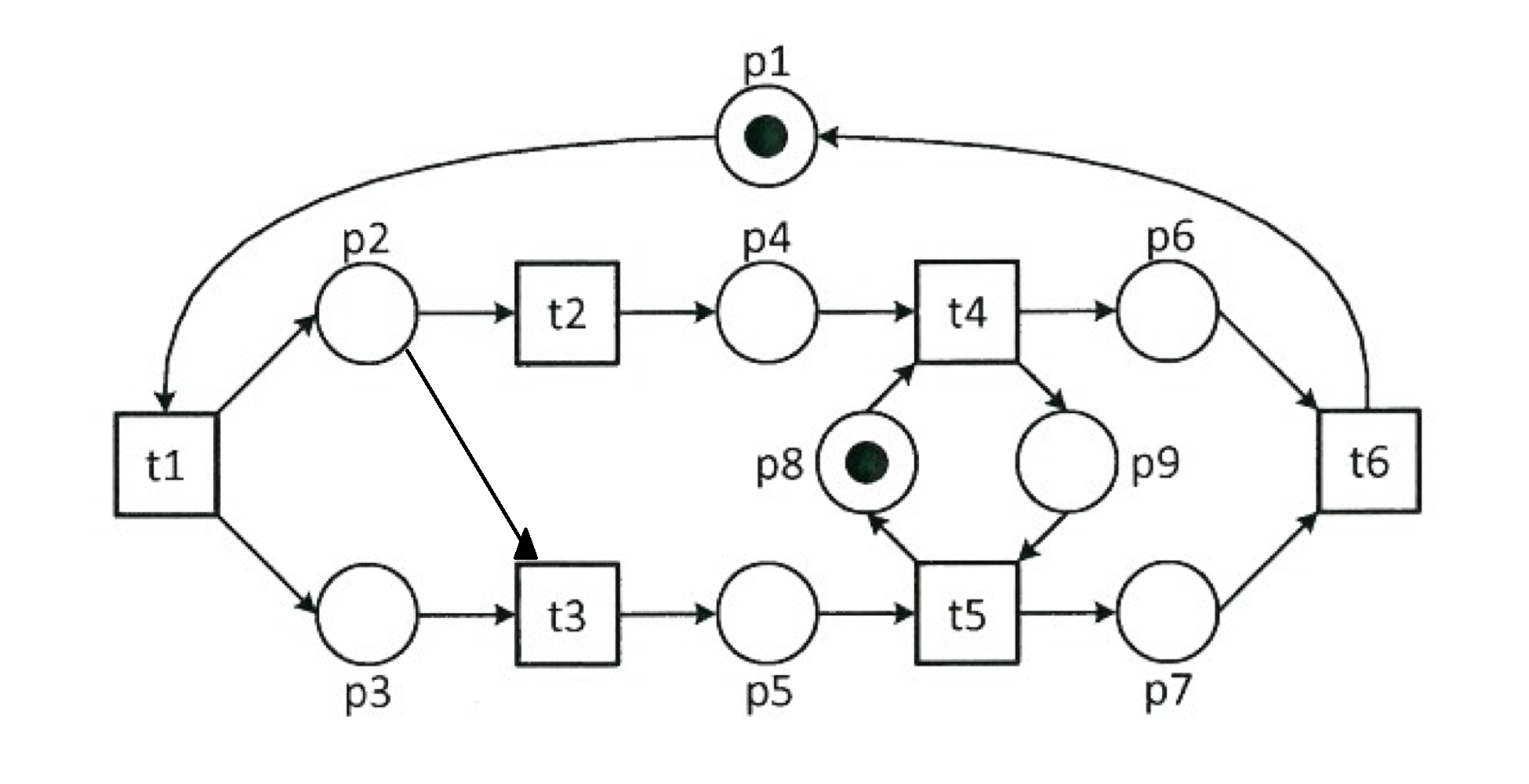
t2의 input place는 p2이고, t3의 input place는 p2와 p3이기 때문에 두 트랜지션의 input place에 교집합이 존재하지만 두 transition의 input place는 다르다. 그러므로 위 페트리 넷은 free-choice net이 아니다.
이번 포스팅에서는 p-net, t-net, free-choice net의 세 가지 페트리 넷의 종류에 대해 살펴보았다. 적지 않은 수의 논문들에서 이러한 페트리 넷의 성질을 가정하고 논리를 펼쳐나가기 때문에, 기본적으로 알아 놓는다면 관련 논문을 좀 더 쉽게 읽을 수 있을 것이다.
References
J. Desel and J. Esparza. Free Choice Petri Nets, volume 40 of Cambridge Tracts in Theoretical Computer Science. Cambridge University Press, Cambridge, UK, 1995.








최근댓글