알파 알고리즘(Alpha Algorithm)은 이벤트 로그로부터 프로세스 모델을 찾는, Process Discovery의 가장 기본이 되는 가장 단순한 알고리즘이다. 여태까지 Process Discovery가 무엇인지를 직관적으로 이해하지 못했다면, 알파 알고리즘을 보고 이를 단번에 이해할 수 있을 것이다. 우선, 결과만 놓고 보면 아래 L1 이벤트 로그에서 밑에 있는 프로세스 모델을 도출할 수 있다. 흥미롭지 않은가?


알파 알고리즘
우선, 알파 알고리즘에서는 이벤트 로그의 요소 중 액티비티의 순서에만 집중한다. 하나의 케이스 안에서 액티비티가 어떤 순서대로 일어났는지에 대한 정보만 필요로 하는 것이다. 그 정보만 나타낸 이벤트 로그의 형태가 바로 아래 형태이다.

Footprint Matrix 만들기
가장 먼저 해야할 일은 이 이벤트 로그의 액티비티 간의 log-based ordering relations를 파악하는 것이다.

어려운 단어와 무슨 수식들이 나오기 시작한다. 이제부터 하나씩 설명할테니 당황할 필요 없다. 액티비티 간의 relation에는 총 4가지 종류가 있다.
첫 번째 relation은 Direct Succession (>)이다. 이는 이벤트 로그 내의 하나의 trace 내에서 바로 뒤에 따라오는 (directly followed) 관계의 액티비티를 의미한다. 예를 들어, 위 로그에서는 (a,b), (b,c), (c,d), (a,c), (c,b), (b,d), (a,e), (e,d)가 이에 해당한다.
두 번째 relation은 Causality(->)이다. 이는 a가 b에 대해서 >이지만, 그 역은 성립하지 않는 경우를 말한다. 예를 들어, 위 로그에서 (b,c)와 (c,b)가 모두 존재하기 때문에 b와 c는 ->의 관계가 아니다. 하지만 (a,b), (c,d), (a,c), (b,d), (a,e), (e,d)는 모두 ->의 관계인 것이다.
세 번째 relation은 Parallel(||)이다. 이는 >에서 ->를 뺀 모두이다. 즉, >의 역이 성립하는 (b,c)와 (c,b)의 관계를 말한다.
네 번째 relation은 Choice(#)이다. 이는 아무 관계가 없다는 것이다. 즉, 위에서 나온 모든 relation의 쌍을 제외한 모든 쌍이 #의 관계이다.
우리의 로그에서 이를 정리하면 다음과 같다.

그렇다면, 이를 이용하여 Footprint Matrix를 만들어야 한다. 이는 정말 간단하다. 그저 모든 액티비티 relation에 대해서 저 relation을 채워 넣으면 된다. 그 결과는 다음과 같다.

알고리즘의 기본 아이디어
알파 알고리즘의 기본 아이디어는 간단하다. 위에서 도출해낸 Footprint Matrix를 가지고 페트리 넷 (Petri Net)의 place를 도출하는 것이다. 이 place의 기본 패턴에는 총 5가지가 있다.
첫 번째는 sequence pattern이다. 이는 단순히 액티비티 a 다음에 액티비티 b가 일어나는, 가장 간단한 패턴이다. 이는 a->b 조건에서 성립한다. (우선, 어느 조건에서 성립하는지는 뒤에서 더 자세히 설명할테니 이해가 되지 않더라도 넘어가도록 한다.)

두 번째는 XOR-split pattern이다. 이는 액티비티 a가 일어난 후, b와 c 액티비티 중 하나만 일어나는 패턴이다. 즉, a 다음에 b가 올 수도 있고, c가 올 수도 있다. 이는 a->b, a->c, b#c 조건에서 성립한다.

세 번째는 AND-split pattern이다. 이는 액티비티 a가 일어난 후, b와 c 액티비티 모두가 일어나는 패턴이다. 이는 a->b, a->c, b||c 조건에서 성립한다.

네 번째는 XOR-join pattern이다. 이는 액티비티 a, b 중 하나가 일어나면 c 액티비티가 일어날 수 있는 패턴이다. 이는 a->c, b->c, a#b 조건에서 성립한다.

다섯 번째는 AND-join pattern이다. 이는 액티비티 a, b가 모두 일어나야 c 액티비티가 일어날 수 있는 패턴이다. 이는 a->c, b->c, a||b 조건에서 성립한다.

위에서 소개한 pattern들을 만들 때 footprint matrix에서 얻을 수 있는 정보만을 이용하여 이들을 도출해낼 수 있다는 것을 알 수 있다. 이것이 알파 알고리즘의 기본적인 아이디어이다.
알고리즘 적용시키기
그렇다면 다시 Footprint Matrix와 이벤트 로그로 돌아가자.


자, 여기서 어떻게 해야 프로세스 모델을 얻을 수 있을까? 알파 알고리즘은 다음과 같다. 수학 같아 보인다고 무서워 할 필요 없다. 하나씩 설명할 것이다.
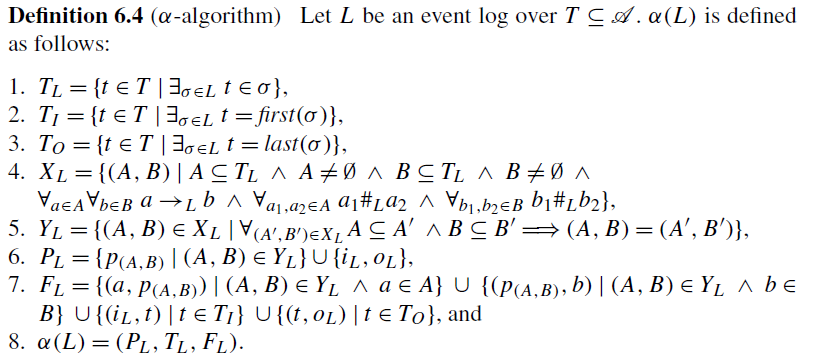
1. T_L을 구한다. 이는 이벤트 로그 내의 모든 액티비티의 집합이다. 즉, 우리의 로그를 예시로 들면 {a,b,c,d,e}이다.
2. T_I를 구한다. 이는 이벤트 로그에서 trace를 시작하는 모든 액티비티이다. 우리의 로그는 항상 a로 시작하기 때문에 {a}이다.
3. T_O를 구한다. 이는 이벤트 로그에서 trace를 끝내는 모든 액티비티이다. 우리의 로그는 항상 d로 끝나기 때문에 {d}이다. 여기까지는 간단하다. 이제 심호흡이 필요하다.
4. X_L을 구한다. 이는 모든 액티비티에 대해 casuality(->) 관계가 있는 집합을 구하는 것이다. 여기에서 조건은, 각 집합 안의 원소들은 서로 choice(#) 관계여야 한다. 우리의 로그를 예시로 들면, ({a}, {b}), ({a}, {c}), ({a}, {b,e})는 가능하지만 ({a}, {b,c})는 b와 c가 # 관계가 아니기 때문에 X_L에포함될 수 없는 것이다.
이를 쉽게 구하기 위해서 내가 주로 쓰는 방법이 있다. 각 행과 열을 하나씩 보는 것이다.
우선, 각 행을 본다. 첫 번째 a 행에서는 b, c, e가 -> 관계를 가진다. 이들로부터 나올 수 있는 부분집합은 {b}, {c}, {e}, {b,c}, {b,e}, {c,e}, {b,c,e}가 있다. 하지만 이 중 b와 c는 # 관계가 아니기 때문에 이들이 포함된 집합인 {b,c}, {b,c,e}는 제외하고 ({a}, {b}), ({a}, {c}), ({a}, {e}), ({a}, {b,e}), ({a}, {c,e})만이 남는다. 두 번째 b 행에서 나올 수 있는 집합은 {d}이기 때문에 ({b}, {d}), c 행에서는 {d}이기 때문에 ({c}, {d}), d 행은 없고, e 행은 ({e}, {d})가 있다.

다음으로, 각 열을 본다. a 열의 경우에는 -> 관계가 없고, b 열에서는 {a} 집합이 나올 수 있기 때문에 ({a}, {b})가 생긴다. (열의 경우에는 열의 기준 액티비티가 뒤로 간다.). c 열에서도 {a}이기 때문에 ({a},{c}) 가 만들어진다. d 열에서는 b,c,e 액티비티가 -> 관계에 있기 때문에 {b}, {c}, {e}, {b,c}, {b,e}, {c,e}, {b,c,e} 집합이 만들어질 수 있는데, 이들 중 b, c는 # 관계가 아니기 때문에 이들이 포함된 집합을 제외하면 {b}, {c}, {e}, {b,e}, {c,e}가 남고, 이에 의해 ({b},{d}), ({c},{d}), ({e},{d}), ({b,e},{d}), ({c,e},{d})가 남는다. e 열에서는 ({a},{e})가 만들어진다.

이제 이 행과 열에서 만들어진 모든 집합의 합집합을 구한다. 그것이 바로 X_L이다. 우리의 이벤트 로그에서 구한 X_L은 다음과 같다.
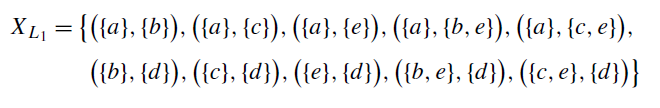
5. Y_L을 구한다. Y_L은 X_L에서 maximal이 아닌 것을 모두 제외한 집합이다. 예를 들어, ({a}, {b}), ({a}, {b,e})의 두 개의 쌍이 있을 때, ({a},{b})는 ({a},{b,e})에 앞, 뒤 원소가 모두 속하기 때문에 maximal이 아니다. 이렇게 maximal을 모두 제거하면 Y_L이 도출된다. 이 Y_L이 페트리 넷의 place의 기준이 된다.

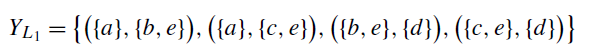
프로세스 모델 도출하기
이제 거의 다 왔다. 정말 간단한 단계만이 남았다.
우선, 시작 place와 끝 place를 만들어 준다.

다음으로, 모든 액티비티, T_L를 표시해 주고, T_I를 start place에, T_O를 end place에 연결해준다.

다음으로, Y_L의 집합들에 해당하는 place들을 만들어준다.

마지막으로, 각 place에 해당하는 arc들을 연결해 준다. 이 때, 각 place의 앞에 오는 것이 place로 들어오는 arc, 뒤에 오는 것이 place에서 나가는 arc이다.
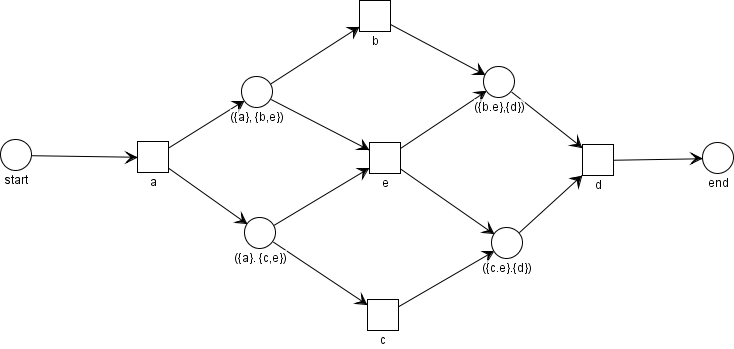
이렇게 프로세스 모델이 완성되었다!!! 이벤트 로그의 액티비티 정보만을 이용해 이렇게 한 눈에 볼 수 있는 프로세스 모델을 도출하다니. 놀라운 일이다.
하지만 이 알파 알고리즘에도 명확한 한계점이 존재한다. 이에 대해 알고 싶다면 다음 포스팅을 참고한다.
2019/06/20 - [Process Mining - Theory/Process Discovery] - 알파 알고리즘의 한계, 문제점
알파 알고리즘의 한계, 문제점
이전에 우리는 알파 알고리즘에 대해 살펴 보았다. 알파 알고리즘은 이벤트 로그로부터 프로세스 모델을 가장 단순한 방법으로 도출해낼 수 있다는 장점을 가지지만, 알파 알고리즘은 몇 가지 치명적인 문제점들을..
process-mining.tistory.com
이 알파 알고리즘을 실제 데이터에 대해 사용해보고 싶다면 다음 포스팅을 참고한다.
2019/07/28 - [Process Mining - Tools/pm4py] - PM4Py로 프로세스 모델 도출하기 (알파 알고리즘)
PM4Py로 프로세스 모델 도출하기 (알파 알고리즘)
데이터를 프로세스 마이닝을 활용하여 분석할 때, 가장 먼저 하는 일은 프로세스 모델 도출일 것이다. (물론 데이터 전처리가 되었다는 가정 하에) 이번 포스팅에서는 pm4py에서 알파 알고리즘을 이용하여 프로세..
process-mining.tistory.com
2019/10/17 - [Process Mining - Tools/ProM] - ProM으로 프로세스 모델 도출하기 (알파 알고리즘)
ProM으로 프로세스 모델 도출하기 (알파 알고리즘)
저엉말 오랜만에 ProM 포스팅. 이번 포스팅에서는 ProM으로 process discovery의 가장 기본적인 알고리즘인 알파 알고리즘으로 프로세스 모델(페트리 넷)을 도출하는 방법에 대해 알아보겠다. * 이 포스팅은 ProM..
process-mining.tistory.com








최근댓글