이 포스팅을 미루고 미뤘던 이유는 지금 연구실에서 내가 하고 있는 것이기 때문이다. 집에서까지 이 친구를 마주치고 싶지 않았다. 워라밸 소중해
우리는 이벤트 로그를 transition system으로 바꿀 수 있다. 이 transition system을 이용해서 우리는 페트리 넷을 도출할 수 있다. 이렇게 transition system의 state를 이용하여 페트리 넷을 도출하는 process discovery 방법을 state based region theory라고 한다. 이번 포스팅에서는 state based region theory가 무엇이고, 어떻게 페트리 넷을 도출하는지에 대해 알아보겠다. transition system이 무엇인지를 모른다면 아래 포스팅을 참고하도록 하자.
2019/06/21 - [Theory/Process Model] - 트랜지션 시스템(Transition System)이란? Reachability Graph란?
트랜지션 시스템(Transition System)이란? Reachability Graph란?
트랜지션 시스템(Transition System)은 프로세스 모델의 한 종류로, 이름에서도 알 수 있 듯이 Transition과 함께 State를 나타내는 것을 목적으로 하는 모델이다. 이 때, state는 페트리 넷의 marking이 될 수도..
process-mining.tistory.com
* 이번 포스팅은 트랜지션 시스템이 Elemenatry Transition System임을 가정한다.
Region
State Based Region Theory에서 state는 트랜지션 시스템의 state일 것이고, based와 theory는 알고 있고, region은 무엇일까? Region은 다음과 같이 정의할 수 있다.

오.. 수학.. 예시와 함께 쉽게 풀어서 설명하도록 하겠다. 정의를 통해 이해할 수 있다면 넘어가도 좋다. 다음과 같은 transition system이 있다고 하자.

ㅇregion은 우선, {s1}, {s2, s4} 등의 state의 집합이다. 근데 이제 여기에 3개의 조건을 곁들인. 이 3개의 조건은 각 액티비티들에 대해서 모두 enter, exit, do not cross의 세 가지의 상태 중 하나만 있어야 한다는 것이다. 이 세가지의 상태에 대해 우선 설명하도록 하겠다. 예를 들어, {s2, s4, s5, s8}이라는 state의 집합이 있다고 하자.

Enter
Enter는 해당 state의 집합이 아닌 곳에서 해당 state의 집합으로 들어가는 transition을 의미한다. 우리의 예시 TS에서 {s2, s4, s5, s8}으로 들어가는 transition에는 a가 있다.
Exit
Exit는 해당 state의 집합에서 해당 state의 집합이 아닌 곳으로 나오는 transition을 의미한다. {s2, s4, s5, s8}에서 나오는 transition에는 b가 있다.
Do not corss
Do not Cross는 해당 state의 집합 아예 바깥쪽에 있거나 아예 안 쪽에 있는 transition을 의미한다. 즉, 해당 state의 집합에서 아닌 곳으로, 혹은 아닌 집합에서 해당 state의 집합인 곳으로 넘어다니지 않는 transition이다. enter와 exit 관계가 아닌 모든 관계를 말하기도 한다. {s2, s4, s5, s8} 안에 있는 transition에는 c, d, 밖에 있는 transition에는 d, c, e가 있기 때문에 이는 {c,d,e}이다.
그렇다면 이 state set은 region일까? 모든 트랜지션 a, b, c, d, e에 대해 enter, exit, do not cross가 하나씩만 나타나는가? a는 enter, b는 exit, c는 do not cross, d는 do not cross, e는 do not cross이기 때문에 답은 예이다. {s2, s4, s5, s8}은 region이다.
하나의 예를 더 들어서 {s2, s3, s4}이 region인지를 확인해 보자.

a, b, c, d, e 트랜지션을 각각 살펴 보자. a 트랜지션은 enter를 한다. b 트랜지션은 s2->s3 부분에서는 do not cross를 하지만, s3->s7에서는 exit를 하고 있다. b 트랜지션에 대해 두 개 이상의 관계 (do not cross, exit)를 가지기 때문에 {s2, s3, s4}는 region이 아니다.
Non-Trivial Region과 Minimal Region
그런데 어떤 트랜지션 시스템이 있을 때, region은 과연 몇 개나 만들어질 수 있을까? 트랜지션 시스템에 액티비티의 개수가 그렇게 많지 않자면 문제가 안 되겠지만, 액티비티의 개수가 많아지면 많아질수록 region의 개수는 기하급수적으로 증가한다. 그렇기 때문에 우리는 트랜지션 시스템에서 모든 region을 고려하는 것이 아니라, non-trivial이고 minimal한 region만 고려하도록 한다.
Non-trivial region
Non-trivial region은 trivial하지 않은 region을 말한다. Trivial Region은, 모든 state를 포함하는 state set과 아무 state도 포함하지 않는 state set을 뜻한다. 우리의 TS를 예로 들자면, {}(아무 state도 포함하지 않는 state set)과 {s1, s2, s3, s4, s5, s6, s7, s8, s9, s10} (모든 state를 포함하는 state set)이 trivial region이다. 이들이 region인 것은, 모든 액티비티 a, b, c, d, e에 대해 do not cross하기 때문이다. 이들은 우리의 고려 대상에서 제외한다.

Minimal Region
Region에는 하나의 성질이 있다. 만약 두 개의 region이 있고 한 region이 다른 한 region의 subset인 경우, 큰 region에서 subset이 되는 region을 빼면 그것 또한 region이라는 성질이다. 아래 그림을 보자.

위 그림에서처럼, {s2, s3, s4, s5, s6, s7, s8, s9, s10}이 region이고 {s2, s4, s5, s8}이 region이면 subset인 {s2, s4, s5, s8}을 뺀 {s3, s6, s7, s9, s10}도 region인 것이다.
Minimal Region은, 그 안에 region이 더 이상 포함되지 않는, 더 작은 region으로 나누어질 수 없는 region을 의미한다. 즉, 위 예시에서 {s2, s3, s4, s5, s6, s7, s8, s9, s10}은 {s2, s4, s5, s8}이라는 region인 subset을 가지기 때문에 minimal region이 아닌 것이다.
우리가 트랜지션 시스템에서 region을 찾을 때에는, non-trivial이고 minimal인 region만 고려하도록 한다.
Petri net Synthesis
이제 기본적인 개념들을 다 알았으니 트랜지션 시스템을 페트리 넷으로 바꾸는 방법을 알아볼 차례이다.
1. 트랜지션 시스템의 모든 트랜지션은 페트리 넷의 transition이 된다.
우리의 TS에서는 a, b, c, d, e의 트랜지션이 있었으므로 이들이 페트리 넷의 트랜지션이 된다.
2. 트랜지션 시스템으로부터 non-trivial이고 minimal인 region을 도출한다.
여기에서는 minimal region을 구하는 방법은 글이 너무 길어지고, 논문을 설명해야 하기 때문에 그것에 대해서는 서술하지 않겠다. 우리의 예시 TS에서는 8개의 minimal non-trivial region이 도출된다.
3. 이 모든 minimal non-trivial region이 페트리 넷의 place가 된다.
우리의 TS에서 8개의 minimal non-trivial region이 도출되었기 때문에 이 8개가 페트리 넷의 place가 된다.
4. arc를 도출한다.
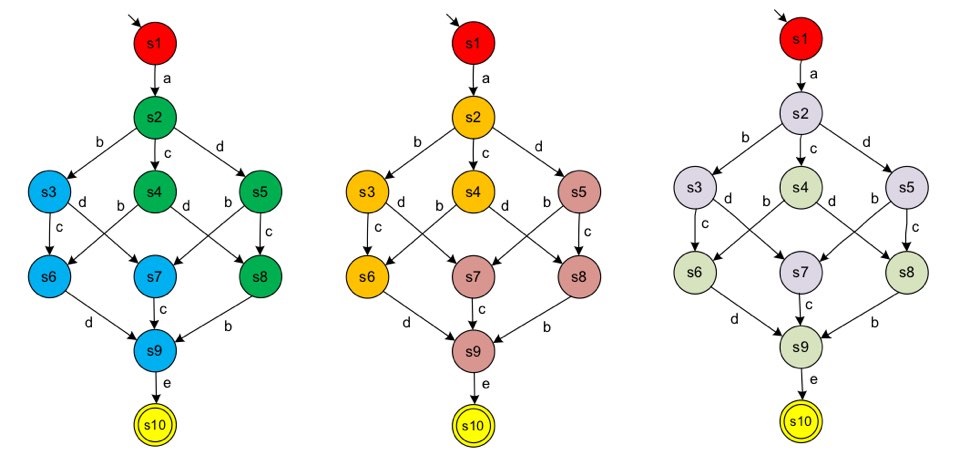
각 minimal non-trivial region에 대해서 어떤 액티비티가 enter하고 어떤 액티비티가 exit하는지를 조사한다. 예를 들어, {s1} (빨간색) 은 a가 exit하고, {s2, s3, s4, s5} (주황색)은 a가 enter하고 d가 exit한다. 그러면 s1에 해당하는 place는 a 트랜지션으로 output(exit이기 때문에) arc를 가지고, {s2, s3, s4, s5}에 해당하는 place는 d 트랜지션으로 output(exit)하고, a 트랜지션이 input한다. 이렇게 각 region에 대해 enter와 exit을 도출하여 arc를 만들면 다음과 같은 결과가 나온다.

5. Initial state에 token을 넣는다.
Initial state가 될 place는 enter하는 트랜지션이 없는 region에 해당하는 place를 말한다. 우리의 경우에서는 {s1}에 해당하는 p1이 initial state이고, 여기에 token을 넣어 주면 된다. 최종 페트리 넷은 다음과 같다. 이렇게 minimal non-trivial region을 바탕으로 하여 도출된 페트리 넷을 Minimal Saturated Net이라고 부른다.

이번 포스팅에서는 트랜지션 시스템으로부터 페트리 넷을 도출하는 state based region theory에 대해 알아 보았다. State Based Region Theory는 이것으로 끝이 아니다. Minimal Region을 찾는 구체적인 알고리즘도 필요하고, Label Splitting이나 Irredundant region들을 제거하는 후처리도 필요하다. 미래의 내가 잘 쓸 것이라고 믿는다. 이거 약간 백종원 아저씨가 유튜브에서 아.. 이 양파볶음으로 카레 맛있게 하는거 있는데. 그건 다음에 알려줄게요. 하고 구독자들에게 기대시키는 느낌.. 물론 백종원 아저씨와는 다르게 나에게는 기대하는 사람이 많지 않다 ㅎㅎ
References
1. Section 7.4.2. of Wil van der Aalst. Process Mining: Data Science in Action (Second Edition) : Springer, 2016.
2. Course: Business Process Intelligence. Wil van der Aalst. RWTH.








최근댓글