어떤 random variable들 X, Y가 있을 때, 우리는 이들이 어떤 관계인지를 궁금해 할 수 있다. 이를 위해 우리는 각 random variable들의 확률 분포가 주어져 있다면 KL divergence를 활용해 이들이 얼마나 비슷한지를 관찰하기도 하고, X, Y의 correlation coefficient를 구하기도 한다. 이번 글에서는 하나의 random variable이 다른 random variable에 얼마나 dependent한지를 나타내는 지표인 mutual information(MI)에 대해서 설명해볼 것이다.
배경 (Correlation의 한계)
서로 다른 두 random variable의 관계를 알고 싶다면, 가장 먼저 우리는 correlation을 계산해볼 수 있을 것이다. 하지만 correlation은 모든 random variable이 real-value인 값을 가지고 있을 때에만 계산할 수 있다는 한계점을 지닌다. 또한 correlation은 두 변수의 dependence를 아주 정확하게는 계산하지 못한다는 단점을 가진다. 아래 그림을 살펴보자.
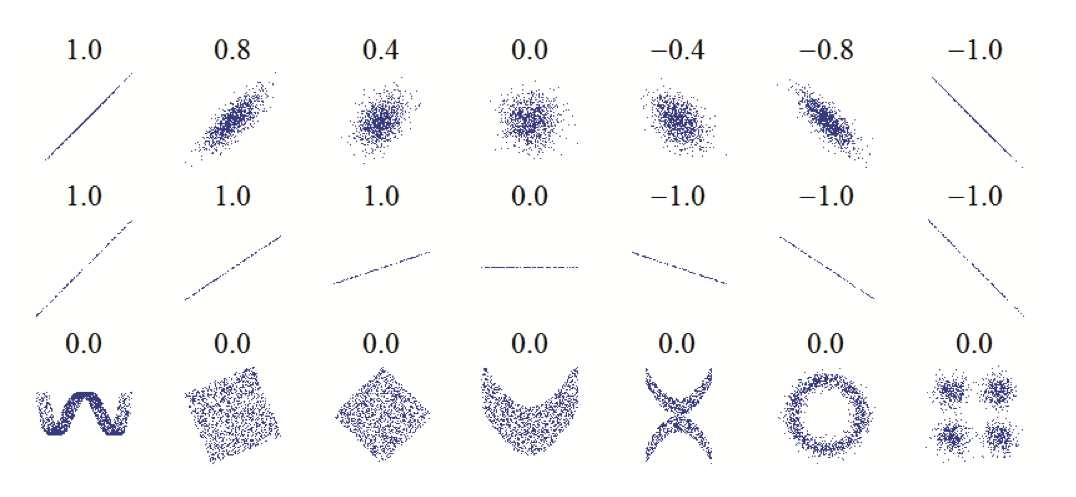
위 그림을 보면, correlation 값이 같아도 분포가 같다고 할 수 없고, 특히 correlation coefficient는 데이터 분포의 경사를 반영할 수 없고(2번째 줄의 그림), 선형적이지 않은 관계는 반영할 수 없다(3번째 줄의 그림)는 한계를 가지는 것을 알 수 있다. 이에 우리는 다른 measure가 필요하다고 생각했고, mutial information이 등장하게 되었다.
정의
Mutual Information은 joint distribution p(X, Y)가 p(X)p(Y)와 얼마나 비슷한지를 측정하는 척도로, 아래와 같이 정의할 수 있다.

이 때, X와 Y가 inpdependent하다면 p(x,y)가 p(x)p(y)와 같아지기 때문에 log 내 식 값이 1이 되고, MI 값은 0이 될 것이다. 그러므로 X, Y가 dependent할수록 MI 값이 커진다고 할 수 있다. 이 때, X와 Y의 순서를 바꾸어도 MI 값은 같다.
해석
Mutual Information 식을 conditional entropy로 다시 표현하면 아래와 같이 표현할 수 있다.

위 식을 해석하면, MI를 X에 대한 uncertainty에서 Y를 알고 난 후에 X에 대한 uncertatinty를 뺀 값이라고 생각할 수 있다. 즉, Y의 정보를 알게됨으로써 X에 대한 불확실성이 얼마나 감소했는지로 해석할 수 있고, 우리는 이를 X가 Y에 대해 얼마나 dependent한지로 해석할 수 있는 것이다.
이제 위 MI와 conditional entropy의 관계식을 증명할 차례이다. (넘어가도 좋다.) 이는 아래와 같이 증명할 수 있다.

Normalized Mutual Information (NMI)
우리가 MI를 사용할 때에 서로 다른 random variable의 집합 간의 dependence를 비교해야 한다면, MI 값에 대한 normalizaiton이 필요한 경우도 있을 것이다. 이를 위해 등장한 개념이 Normalized Mutual Information이다. 우선, 우리가 위에서 유도한 MI와 conditional entropy의 관계식 특성을 살펴보겠다.

그러므로 MI 값은 H(X)와 H(Y) 값보다 작고, 이를 달리 말하면 H(X)와 H(Y)의 최솟값보다 MI 값이 작다고 할 수 있을 것이다. 그러므로 우리는, normalized mutual information을 아래와 같이 정의할 수 있다.
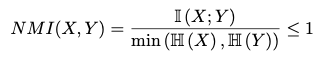
NMI 값이 0이면 I(X;Y)가 0이므로 X와 Y는 independent하다고 할 수 있을 것이다. 반대로, H(X) < H(Y)인 상황에서 NMI 값이 1이면 I(X;Y) 값이 H(X)와 같으므로 H(X|Y)가 0이고, X는 Y에 의해 완전히 결정된다고 볼 수 있을 것이다.
하지만 X, Y 값이 continuous random variable이거나 분포를 알 수 없는 real value인 경우에는 어떻게 NMI 값을 얻을 수 있을까? conditional entropy 값을 명확히 계산하기가 힘들기 때문에 NMI를 계산하는 것이 불가능할 것이다. 이에 등장한 개념이 Maximal Information Coefficient(MIC)이다.
Maximal Information Coefficient (MIC)
X, Y 값이 주어져있는데 분포를 알 수 없을 때 우리는 히스토그램을 그려서 해당 분포를 추정하는 방법을 사용한다. 이와 비슷한 형태로, 우리는 X, Y 값을 discretize하여 각 값을 하나의 bin 안으로 매핑하고, 이를 이용하여 MI를 계산한다. Maxmial Information Coefficient는 다음과 같이 정의할 수 있다.
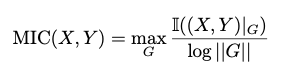
위 식에서 G는 X와 Y 값을 각 bin으로 나눈 2d grid, (X,Y)|G는 각 X,Y 값이 이 grid에 들어간 분포, 그리고 ||G||는 X 방향 grid의 개수와 Y 방향 grid의 개수 중 최솟값을 말한다. log||G||로 값을 normalization 함으로써 MIC 값이 0과 1 사이로 제한되게 된다.

MI와 Correlation
이제 MI가 correlation의 단점을 극복할 수 있다는 것을 설명할 차례이다. 아래 그림은 MIC 값과 Correlation 값을 매핑한 예시이다.

위 그림을 살펴보면, MIC와 correlation이 모두 낮은 C 그림에서는 데이터 안에서 아무런 관계가 없음을, MIC와 correlation이 모두 높은 D, H 그림에서는 linear relationship을, correlation이 낮고 MIC가 높은 E, F, G 그림에서는 correlation이 발견하지 못하는 non-linear relationship을 MIC는 잘 캐치했음을 알 수 있다.
이번 포스팅에서는 하나의 random variable이 다른 random variable에 얼마나 dependent한지를 나타내는 지표인 mutual information(MI)에 대해서 알아보았다. 두 변수 간의 선형 관계뿐만이 아니라 다양한 관계를 도출해낼 수 있는 MI를 잘 활용하면 좋은 분석을 할 수 있을 것이다.
References
1. Probabilistic Machine Learning: An Introduction by Kevin Patrick Murphy. MIT Press, February 2022.
2. Machine Learning: a Probabilistic Perspective by Kevin Patrick Murphy. MIT Press, 2012.








최근댓글