Junction tree VAE (JT-VAE)는 graph generative model의 하나로, 그래프를 원자가 아닌 조금 더 큰 단위의 scaffold로 쪼개서, tree 형태로 decomposition하여 이에 대해 VAE를 적용함으로써 그래프를 생성하는 모델을 말한다. 이번 글에서는 JT-VAE가 무엇인지에 대해서 Junction Tree Variational Autoencoder for Molecular Graph Generation 논문을 리뷰하면서 알아보겠다.
배경
우선, JT-VAE가 제안된 배경에 대해 먼저 살펴보겠다. 아래 그림과 같은 두 개의 분자가 있다고 하자. 두 분자는 실제 그래프로 표현되었을 때의 분자 구조가 아주 비슷하지만, 이를 SMILES로 표현하면 아주 다른 형태의 string이 된다.

이렇게 SMILES는 분자 간의 similarity를 제대로 capture하지 못한다는 한계점을 가지고 있을 뿐더러, 분자가 가지고 있는 chemical property를 잘 표현하지 못한다는 단점을 가진다. 그렇기 때문에 SMILES가 아닌 그래프 형태 자체를 활용해서 그래프를 생성함으로써 더 정확하게 그래프를 만들어낼 수 있을 것이다. 그래서 이 연구는 그래프를 그래프의 구조를 그대로 표현할 수 있는 junction tree 형태로 변환하고, 이 junction tree를 continous한 representation으로 표현함으로써 새로운 그래프들을 생성한다.
Approach
JT-VAE의 방법론을 한 줄로 요약하면, 그래프를 subgraph로 구성된 junction tree 형태로 표현하고, 이 junction tree를 continuous한 representation으로 매핑하여 VAE를 학습하는 것이다. 이를 그림으로 표현하면 아래와 같다.
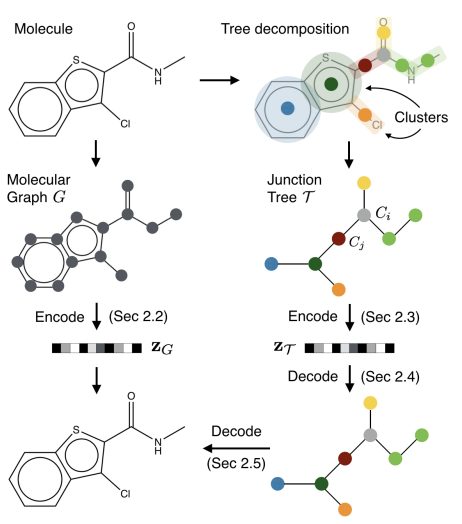
이 과정은 크게 1) 분자를 junction tree 형태로 표현하는 tree decomposition, 2) 그래프 전체를 continous representation으로 매핑하는 graph encoder, 3) junction tree를 continous한 representation으로 매핑하는 tree encoder, 4) continous representation으로부터 junction tree를 매핑하는 tree decoder, 5) junction tree와 continous graph representation으로부터 새로운 그래프를 generate하는 graph encoder의 다섯 가지 부분으로 나눌 수 있다. 이들에 대해서 하나씩 살펴보겠다.
Tree decomposition
첫 번째로, 분자를 tree decomposition을 통해서 junction tree 형태로 변환해야 한다. 이 때, junction tree는 어떤 노드나 엣지들의 집합인 cluster로 구성된 tree 형태를 가진다. 이를 형성하는 과정은 다음과 같다.

- 어떤 분자 그래프에 대해서 모든 cycle들과 그것에 속하지 않는 엣지들을 찾는다. 이 각각의 cycle 혹은 엣지를 하나의 클러스터라고 부른다.
- 각 클러스터들에 대해서 겹치는 부분이 있는 경우, 클러스터 간의 엣지를 만들어서 cluster graph를 생성한다.
- Cluster graph에 대해서 spanning tree를 만들고, 이를 junction tree라고 부른다.

이렇게 tree decomposition 과정을 통해서 junction tree를 만드는 것을 통해 우리는 cluster로 구성된 그래프를 얻게 되고, 아래 그림처럼 invalid한 graph generation step을 거치지 않을 수 있다. 그럼으로써 만약 아래 그림처럼 어떤 ring을 만들어야한다고 할 때, 노드 하나하나씩 generate함으로써 ring이 아닌 잘못된 구조를 만들어낼 가능성을 낮추는 효과를 얻는다.

Graph encoder
두 번째로, graph encoder는 그래프 전체를 continous representation $z_G$로 매핑한다. 이러한 graph encoder는 message passing network를 활용한다.

이 message passing network의 구조는 다음과 같다. 우선, 다음과 같은 식을 통해서 노드 $u$로부터 노드 $v$로 전달하는 message vector를 구성한다. 이 때, $x_u$는 노드 u의 feature vector, $x_{uv}$는 엣지 uv의 bond type을 의미한다.
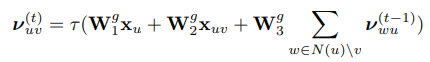
위 식을 $T$번 반복해서 message vector를 계산한 이후에, 이를 활용해 각 노드의 latent vector를 아래 식과 같이 계산한다.

마지막으로, 위로부터 계산한 각 노드의 latent vector를 활용해서 최종적인 graph representation을 아래 식과 같이 도출한다.

위로부터 얻은 최종 graph representation을 input으로 하는 두 개의 affine layer (fully-connected layer)를 통과한 값으로 mean과 variance를 계산하고, 이를 평균과 분산으로 하는 정규분포로부터 샘플링을 통해 graph의 continous representation $z_G$를 얻는다.
Tree encoder
세 번째로, tree encoder는 junction tree를 continous한 representation $z_T$로 매핑한다. 이러한 tree encoder는 tree에 대한 message passing network를 이용한다.

이 때, 각 클러스터는 클러스터의 종류(label)를 표현하는 one-hot vector $x_i$로 표현되고, message는 다음과 같은 message vector를 통해 update된다. 이 때, message들은 두 개의 phase를 통해서 passing된다. 우선 어떤 임의의 leaf 클러스터를 root 노드로 지정하고, 다른 leaf 클러스터들로부터 root를 향해 passing된다. 다음으로, root로부터 다른 모든 leaf 클러스터들을 향해서 passing된다.
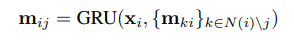
위의 GRU(Gated Rooted Unit)는 다음과 같이 tree message passing에 적합한 형태로 쓰인다.

위 식을 통해 message vector를 계산한 이후에, 이를 활용해 각 클러스터의 latent vector를 아래 식과 같이 계산한다.
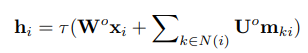
마지막으로, 위로부터 계산한 각 클러스터의 latent vector를 활용해서 최종적인 tree representation을 아래 식과 같이 도출한다. 이 때, graph encoder와 다르게 root 클러스터의 latent vector만을 tree representation으로 사용하는데, 이는 tree decoder 단계에서 root 클러스터를 시작으로 해서 graph를 generate해야하기 때문에, root 클러스터가 무엇인지를 명확하게 하기 위해서이다.

Graph encoder와 동일하게, 위로부터 얻은 최종 graph representation을 input으로 하는 두 개의 affine layer (fully-connected layer)를 통과한 값으로 mean과 variance를 계산하고, 이를 평균과 분산으로 하는 정규분포로부터 샘플링을 통해 graph의 continous representation $z_T$를 얻는다.
Tree decoder
네 번째로, tree decoder는 tree의 continous representation $z_T$로부터 junction tree를 매핑한다.
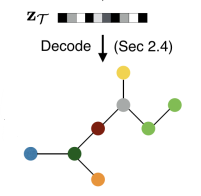
이 tree decoder는 root 클러스터를 시작으로 하여서 root 클러스터의 children 클러스터를 depth-first 방식으로 generate하는 과정을 통해서 junction tree를 만들어낸다. 이를 위해서 우선 다음과 같은 message passing 과정을 거친다. 이 때, $\tilde{\mathcal{E}}$는 depth-first 과정에서 거친 엣지들의 집합을 의미한다.

각 엣지에 대한 message를 구했으면, 노드에 대해서 children node를 가지고 있는지 없는지를 판단하는 topological prediction을 거친다. 어떤 노드 $i_t$가 children이 있을 확률은 다음과 같은 식을 통해서 구한다.

만약 위 식을 통해서 childern 노드 $j$가 만들어졌다면, 이 노드의 label, 즉 클러스터의 종류는 다음 식을 통해서 구한다.
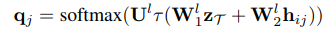
위 식들을 활용해서 decoder를 학습할 때는 아래와 같은 cross entropy loss를 최소화하는 방향으로 decoder를 학습한다. 이 때, 아래 식에서 hat이 있는 p와 q는 ground truth를 의미한다. 즉, 아래 식은 실제 ground truth junction tree와 generate되는 junction tree가 가장 비슷한 방향으로 decoder가 학습되는 것을 뜻하는 것이다.
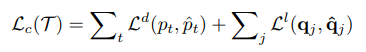
Tree decoder가 학습되는 과정을 예시를 통해서 알아보면 다음과 같다. 우선, 노드 2에 대해서 children이 있는지를 topological prediction을 통해서 예측한다. 이 때, children 노드 4가 있다는 결론이 나와서 노드 4가 만들어지고, message $h_{24}$를 통해 노드 4의 label을 예측한다. 다음으로, 노드 4는 더 이상 children이 없는 leaf 노드이기 때문에 $h_{42}$의 message를 계산한다. 계속 backtracking을 진행하고, root에 도달한다면 이 root가 추가적인 children이 있는지 확인한다. 있다면, 위 과정을 반복한다.

이를 알고리즘으로 나타내면 다음과 같다.

Graph decoder
마지막으로, graph decoder는 도출된 junction tree와 graph representation $z_G$를 활용해서 그래프를 매핑한다.

이 때, input으로 받는 junction tree는 cluster 간의 연결만을 표현하기 때문에, 같은 junction tree에서도 다른 그래프 형태가 도출될 수 있다. 그러므로 graph decoder는 같은 클러스터를 가지고 있는 그래프들 중 가장 적절한 그래프를 찾아내는 역할을 한다. 이를 식으로 나타내면 다음과 같다.

Graph decoder가 그래프를 만들어내는 과정은 다음과 같다.

이 때, tree decoder가 만들어진 것과 같은 순서로 클러스터를 더해간다. 클러스터 i와 이에 이웃하는 클러스터들 j들을 합해서 하나의 subgraph $G_i$를 만든다. 이 subgraph의 score를 다음과 같은 식을 통해 도출한다.

도출된 subgraph의 score 중 가장 높은 score를 가지는 subgraph를 선택한다. 이 과정을 반복함으로써 각 클러스터에 알맞은 노드들의 구조를 선택한다.
Experiment
JT-VAE가 얼마나 잘 작동하는지에 대해서 몇 가지 실험을 통해 알아보겠다.
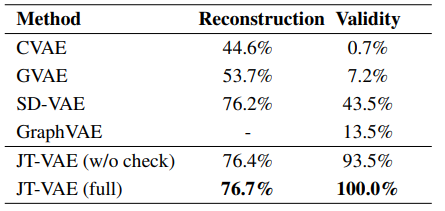
우선, JT-VAE는 기존의 VAE를 활용한 연구들보다 reconstruction accuracy가 높고, valid한 분자들을 더 잘 만들어냈다. 이를 증명하는 실험 결과는 아래와 같다.
또한 JT-VAE는 특정 property를 optimize하는 것에도 좋은 성능을 가지고 있는 것으로 드러났다. 이의 결과는 아래와 같다.

이번 글을 통해 우리는 JT-VAE가 어떻게 작동하는지에 대해 알아보았다.
References
Jin, W., Barzilay, R., & Jaakkola, T. (2018, July). Junction tree variational autoencoder for molecular graph generation. In International conference on machine learning (pp. 2323-2332). PMLR.








최근댓글