Graph convolutional network (GCN)은 가장 기본이 되는 graph neural network 중 하나로, CNN의 local feature를 학습한다는 특징과 weight sharing을 그래프에 적용시키는 neural network이다. 이번 글에서는 GCN이 무엇인지와 함께 GCN이 어떻게 작동하는지에 대해서 설명하고, 다음 글에서는 GCN의 구조가 왜 그렇게 되었는지에 대해서 좀 더 구체적으로 설명하도록 하겠다.
Motivation
들어가기에 앞서, GCN의 motivation에 대해서 간략하게 설명하도록 하겠다. Convolutional neural network (CNN)은 사진 데이터에 가장 널리 사용되는 neural network 구조로써, local feature를 학습하고 weight sharing을 특징으로 가진다. 아래 그림과 같이 CNN은 한칸씩 옮겨가며 해당 칸의 feature들을 aggregation함으로써 local feature로 사용한다.

그리고 CNN은, 각 feature들마다 다른 neural network를 사용하는 것이 아닌, weight를 공유하는 neural network를 사용함으로써 효율적으로 파라미터를 사용한다.
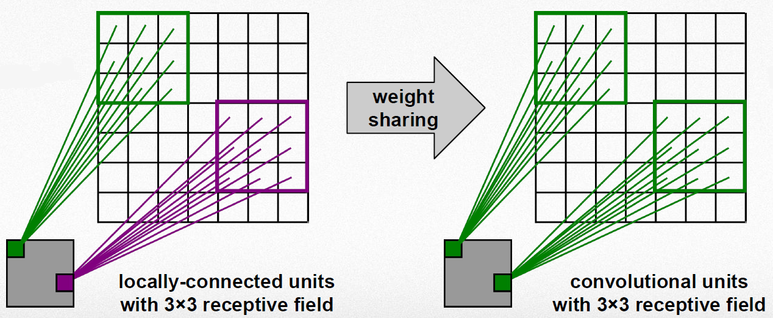
하지만 이러한 CNN 구조를 그대로 그래프 데이터에 사용하기 위해서는 어려움이 있다. 그 이유는, 그래프 데이터의 경우 이웃하는 노드의 개수가 CNN과 다르게 일정하지 않고, 그래프의 노드들의 순서가 바뀌었을 때도 output이 일정하게 유지되는 permutation invariance가 유지되어야 하기 때문이다. 그래서 그래프 데이터에 대해 CNN과 비슷한 특성을 가지는 neural network가 고안되었고, 이것이 바로 GCN이다.
정의
GCN은 어떤 input graph에 대해서 각 노드의 label을 예측하는 neural network로, 다음과 같은 식을 통해서 hidden state를 업데이트한다.

위 식에서 $H^{(l)}$은 $l$번째 hidden layer의 hidden state 행렬, $\tilde{A}$는 adjacency matrix에 identity matrix를 더한, self connection이 포함된 adjacency matrix, $\tilde{D}$는 degree matrix에 identity matrix를 더한 것, 그리고 $W$는 weight matrix를 의미한다. 위 식에서 앞의 $\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}$는 계산해보면 서로 노드가 연결되어 있거나 행과 열이 같을 때에만 값이 있고 나머지는 0인 행렬이고, H는 노드의 개수 X feature의 개수 행렬, W는 feature의 개수 X weight의 개수 행렬이다.
위 정의를 예시와 함께 살펴보자. 예를 들어서, 다음과 같은 그래프가 있다고 하자.

위 그래프의 feature 개수가 5, weight의 개수가 3이라고 할 때 GCN의 구조에 포함되는 행렬들은 아래 그림과 같은 구조를 가진다.
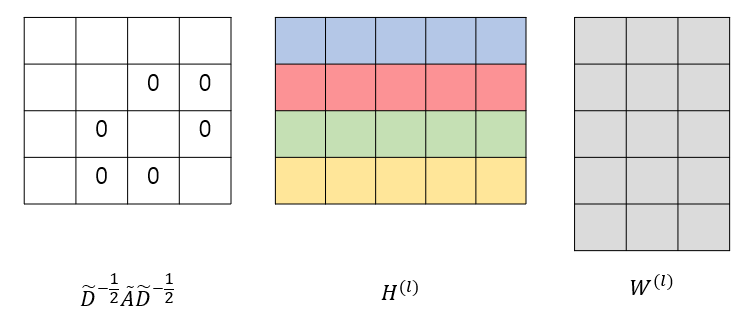
위 그래프의 $\tilde{A}$와 $\tilde{D}$는 아래 식을 통해서 계산된다.

그러므로 위 GCN의 정의를 예시 그래프에 대해서 다시 쓰면 다음과 같다.

예를 들어, 우리가 노드 1의 hidden layer 값을 구하고 싶다고 하자. 위 식에 따라서 계산하면, 노드 1은 다음과 같은 식에 따라 hidden layer가 계산될 것이다. (상수는 생략한다.)

다음으로, 노드 2의 hidden layer 값을 구하고 싶다고 하자. 위 식에 따라서 계산하면, 노드 2는 다음과 같은 식에 따라 hidden layer가 계산될 것이다. (상수는 생략한다.)

이와 같이 각 노드는 이웃한 노드와 본인 노드의 hidden layer 값만을 이용해서 계속 값을 update해나갈 것이고, 이는 CNN이 local feature를 사용하는 특성과 비슷하다. 또한 이 각각의 이웃 노드들을 업데이트할 때는 같은 weight matrix를 사용하고, 이는 CNN의 weight shariing 특성과 비슷하다고 할 수 있다.
구조
마지막으로, GCN 네트워크의 전체적인 구조에 대해서 살펴보겠다. GCN 네트워크는 다음과 같은 구조를 가진다.
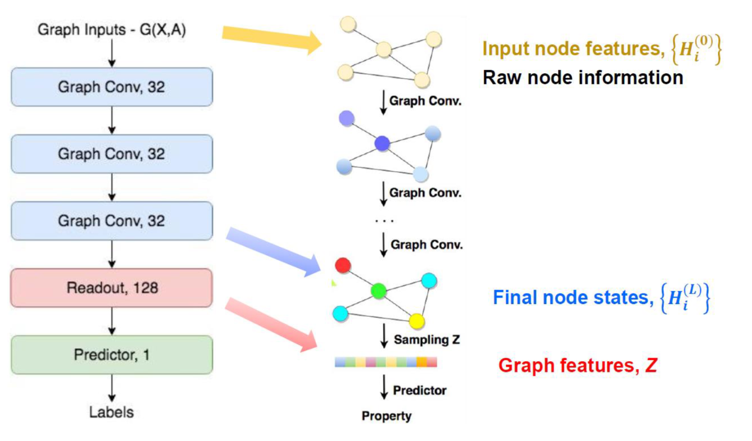
위 구조에서 Graph Conv는 위에서 설명했던 GCN이 hidden layer를 update했던 그 layer를 의미한다. 우리가 위 구조에서 눈여겨봐야할 점은 크게 두 가지이다. 첫 번째로, 그래프가 input으로 node feature와 함께 adjacency matrix를 함께 받는다는 것이다. 이를 통해 우리는, node feature만으로 표현할 수 없는 정보를 adjacency matrix를 통해 받게 되고, 이웃한 노드들끼리 비슷한 label을 가진다는 가정 아래에서 더 잘 작동하는 classification 모델을 얻게 된다. 두 번째로, readout이 permutation invariance를 지킬 수 있는 함수여야한다는 점이다. 노드의 순서가 바뀐다고 해서 노드들의 label이 바뀌면 안되기 때문에, permutation invariance를 지킬 수 있는 노드들 전체의 합 등을 readout으로 사용하게 된다. 이 readout은 graph 전체의 특성을 예측하는 graph classification 등에서만 사용된다.

이번 글에서 우리는 GCN이 무엇이고, 이것이 어떻게 작동하는지에 대해서 알아보았다. 다음 글에서는 GCN이 왜 저런 형태를 가지게 되었는지에 대해서 spectral graph convolution 개념과 함께 좀 더 구체적으로 알아보겠다.
References
1. Kipf, T. N., & Welling, M. (2016). Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907.
2. https://www.ibm.com/cloud/learn/convolutional-neural-networks








최근댓글