NCSN은 noise conditional score network의 줄임말로, 데이터를 점점 더 작아지는 노이즈로 perturb함으로써 기존 score matching의 문제를 해결한 최초의 높은 성능의 score-based diffusion model이다. Yang Song의 Generative modeling by estimating gradients of the data distribution 논문에서 처음 제시된 개념으로, score-based diffusion model들의 가장 기본이 되는 모델이다. 이번 글에서는 이러한 NCSN이 무엇인지에 대해 알아보겠다.
Recap
이 글을 이해하기 위해서는 score matching과 Langevin dynamics에 대한 이해가 필수적이다. 여기에서는 기억력을 되살리기 위해서 둘에 대한 간단한 요약만 진행하겠다.
Score matching
Score matching은 log-likelihood의 gradient인 score function을 학습함으로써 probability density function을 추정하는 것을 의미한다. Score matching의 objective는 다음과 같이 정의된다.

이를 좀 더 계산이 쉽게 정리하면 다음과 같다.

Langevin dynamics
Langevin dynamics는 score matching에서 구한 score function을 활용하여 데이터를 샘플링(혹은 생성)하는 방법이다. 가장 간단한 방법으로, 아래와 같은 식의 Euler-Maruyama method를 활용하여 샘플링이 가능하다.
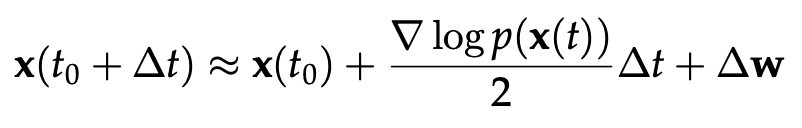
Motivation
기존의 아주 간단한 형태의 score-based 생성 모델은 위에서 설명한 score matching 식을 활용하여 학습을 진행하고, 이를 통해 학습한 score function을 Langevin dynamics 식에 넣음으로써 샘플링을 진행해왔다. 하지만 이러한 방법들은 몇 개의 한계점을 가진다.

첫 번째 한계점은 trace의 계산이 굉장히 복잡하다는 것이다. 우리가 score matching의 objective에 있는 trace를 계산하고 학습을 진행하려면 항상 dimension 개수만큼의 back propagation을 해야 한다는 문제점을 가진다. 이러한 계산은 너무 복잡하기 때문에 이미지와 같은 높은 디멘션을 가지는 데이터에 score matching을 적용하는 것이 현실적으로 불가능해진다.


두 번째 한계점은 probability density가 낮은 곳에서는 제대로 score estimation을 할 수 없다는 점이다. 우리가 위에서 정의한 Fischer divergence는 아래 식과 같이 data distribution에 대한 기댓값으로 정의된다.

그렇기 때문에 data가 몇 개 없는 곳, 즉 probability density가 낮은 곳에 대해서는 상대적으로 작은 weight를 가하게 되고 이에 따라 이 부분에 대해서는 정확한 score estimation이 어렵다. 따라서 만약 맨 처음에 시작을 low density region에서 하게 되면 이곳의 score가 정확하지 않기 때문에 끝까지 높은 질의 샘플을 얻기가 힘든 것이다.

Noise conditional score networks
이러한 문제점들을 해결하기 위해서 noise conditioned score network, 즉 NCSN이 등장했다. NCSN은 실제 true data distribution을 학습하는 것을 포기하고, noise로 perturbed된 data distribution을 학습함으로써 위에서 나타났던 문제들을 해결한다. 이러한 과정을 우리는 denoising score matching이라고 부른다.

Denoising score matching
Denoising score matching은 score matchiing을 하는데, 이 score matching이 noise를 없애는 역할(denoising)을 하는 것을 의미한다. 이는 위에서 설명한 것처럼 noise perturbed distribution을 학습함으로써 1) trace의 계산을 피하고, 2) probability density가 낮은 곳을 줄여주는 역할을 한다. 지금부터 어떻게 이런 작용을 할 수 있는지에 대해 알아보겠다.
우선, 우리가 학습을 목적으로 하는 noise perturbed distribution은 다음과 같이 정의할 수 있다. 즉, 어떤 데이터 $x$가 주어졌을 때, 이것의 perturbed 데이터인 $\tilde{x}$의 분포를 학습하는 것이다.

이 식을 활용해 우리의 denoising score matching objective를 다시 써보면 다음과 같은 식이 된다. 즉, x라는 데이터가 주어졌을 때의 perturbed x의 likelihood를 증가시키는 것이 perturbed x의 likelihood를 증가시키는 것과 같은 것이다.

위 식과 아래 식이 같은 것에 대한 증명은 다음과 같이 할 수 있다. (생략 가능)

결과적으로, 우리가 원하는 denoising score matching의 objective는 다음과 같은 식이 된다.

이것의 계산을 용이하게 하기 위해서 우리가 x가 주어졌을 때의 perturbed x의 확률 분포가 다음과 같은 정규 분포를 따르는 Gaussian perturbation이라고 가정하자.

그러면 우리의 objective는 다음과 같은 쉬운 형태로 정리될 수 있을 것이다.

이러한 trace의 계산이 필요 없는 objective가 정의됨으로써 우리는 trace의 계산을 피할 수 있다. 또한 noise가 가해진 형태의 perturbed data distribution을 추정함으로써 우리는 데이터가 굉장히 low density였던 곳도 다음 그림과 같이 어느 정도의 density를 가지는 형태로 변환할 수 있다. 즉, probability density가 낮은 곳을 줄여주는 역할을 하는 것이다. 뿐만 아니라, score network s의 형태가 정해져 있지 않기 때문에 우리가 원하는 어떤 모델이든 사용이 가능하다는 장점도 가진다.

Multiple scales of noise perturbations
그렇다면 우리는 이 noise의 크기를 어떻게 적절하게 정할 수 있을까? Noise가 크면 low density region을 더 많이 커버할 수 있지만, 실제 data distribution을 너무 많이 perturb한다는 단점을 가진다. 반대로 noise가 작으면 original data distribution에 비교적 작은 corruption을 할 수 있지만, low density region을 많이 커버할 수 없다는 단점을 가진다. 이러한 두 상황의 장점을 모두 취하기 위해, 우리는 아래 그림과 같이 noise의 variance가 점점 커지는 형태로 이를 정의한다.

하지만 이렇게 noise의 scale이 단계마다 다르면 각 단계마다의 objective의 크기가 달라질 수 있다. 그렇기 때문에 각 단계마다 적절한 weight를 가해서 objective를 더해줄 필요가 있다. 그 형태는 아래와 같다.

여기에서 weight $\lambda$는 보통 $\sigma$의 제곱으로 정의되는데, 이는 score network가 실험적으로 $1/\sigma$에 비례하기 때문에 이를 보정하기 위해서이다.
Inference (Sampling) with annealed Langevin dynamics
Score network의 학습이 끝나고 이를 활용해서 샘플링을 할 때에는 학습한 score network를 활용해 Langevin dynamics를 활용한다. 즉, Langevin dynamics의 score function 부분에 학습한 score network를 대입하는 것이다.
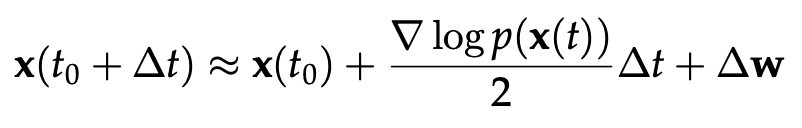
하지만 우리는 다음과 같이 다양한 scale의 noise에 대해서 각각 다른 score function 값을 가지게 된다.
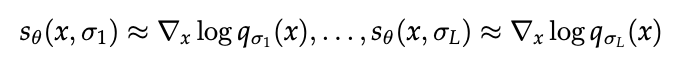
앞서 설명한 것처럼, noise가 크면 low density region을 더 많이 커버할 수 있지만, 실제 data distribution을 너무 많이 perturb한다는 단점을 가진다. 반대로 noise가 작으면 original data distribution에 비교적 작은 corruption을 할 수 있지만, low density region을 많이 커버할 수 없다는 단점을 가진다. 샘플링을 할 때에도 이러한 noise의 특성을 반영하기 위해 처음에는 큰 noise로 low density function을 커버한 후에, 작은 noise로 정확한 density estimation을 하는 방식으로 샘플링을 진행한다. 이를 알고리즘으로 표현하면 다음과 같다.

Experiments
이러한 NCSN을 통해 이미지를 생성하면, GAN과 비슷한 성능의 높은 퀄리티의 이미지를 생성할 수 있다. 지금이야 GAN이 좀 오래된 모델로 여겨지지만, NCSN이 발표될 당시만 해도 GAN이 이미지 생성의 왕 느낌으로 군림하고 있었기 떄문에 이러한 성능은 생성 모델계에서 괄목할 만한 성과였다고 할 수 있다.

이번 글을 통해 우리는 NCSN, 즉 noise conditional score network가 무엇인지에 대해 알아보았다. 다음 글에서는 SDE를 활용해 noise conditional score network의 성능을 더 끌어 올린 score matching with SDE에 대해 알아보겠다.
References
1. https://yang-song.net/blog/2021/score/
2. Slides in a seminar in Ahn lab. (by Dongyeop Woo)








최근댓글