Euler-Maruyama method는 SDE의 해를 쉽고 간단하게 근사하는 방법으로, ODE의 해를 근사하는 Euler method를 SDE에 맞게 확장시킨 방법이다. Euler-Maruyama method도 Euler method와 비슷하게 아주 작은 스텝을 이동하면서 값이 어떻게 바뀌는지를 활용하여 해를 근사한다. 이번 글에서는 Euler-Maruyama method가 무엇인지에 대해 알아보겠다.
Motivation
다음과 같은 SDE의 해를 구하는 것이 목적이라고 하자. 이는 다시 말해, 아래와 같은 식이 주어졌을 때 특정 시점 $t$의 $x(t)$ 값을 구하는 것이 목적인 것이다.

이러한 식을 바로 적분을 통해서 직접적으로 풀기 위해서는 다음과 같은 식을 해결하면 된다.

하지만 이러한 식을 푸는 것은 굉장히 복잡한 계산을 동반하기 때문에 쉽지 않다. 그래서 우리는 Euler method와 비슷한 방법으로, 어떤 작은 timestep $\Delta t$를 이동했을 때의 first-order Taylor expansion을 활용한다. 이는 다음과 같은 식으로 표현된다.
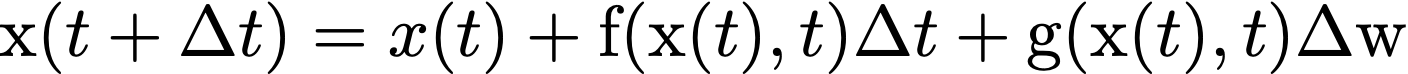
이 형태를 활용해서 우리는 $x(t)$의 값을 단계적으로 업데이트하게 되고, 최종적으로 SDE의 해를 근사할 수 있게 되는 것이다.
Euler-Maruyama method
Euler-Maruyama method는 Euler method처럼 함수를 아주 작은 step으로 쪼개어 discretize하고, 현재의 값을 이용하여 다음 스텝의 값을 approximate한다. 이를 통해 우리는 우리가 원하는 커브를 구할 수 있게 된다. Euler-Maruyama method가 진행되는 순서는 다음과 같다.
1. Initial condition $x(t_0)$와 fixed step size $\Delta t$를 정한다.
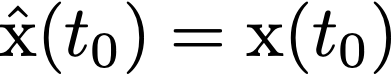
2. 정해진 step size를 활용하여 Wiener process로부터 $\Delta \mathrm{w}$를 샘플링한다.

3. 이 값을 활용하여 다음과 같은 식을 통해 다음 스텝에서의 $x(t_{k+1}$을 근사한다. (이 식은 위의 first-order Taylor expansion 식을 따른다.)

4. 2와 3 과정을 반복한다.
위 과정을 우리가 원하는 마지막 point까지 반복하는 것을 통해 우리는 우리가 원하는 함수 $x(t)$를 근사할 수 있다.
이번 글에서는 Euler-Maruyama method에 대해 알아보았다. Euler-Maruyama method는 굉장히 쉬운 방법임에도 적당히 step size가 크면 값을 잘 근사할 수 있기 때문에 SDE의 근사를 위해 널리 활용된다.








최근댓글