이번 포스팅에서는 Maximum Likelihood가 무엇인지에 대해 알아보겠다. 이 포스팅은 정규 분포에 대한 이해가 있다고 가정한다.
Likekihood
Likelihood란, 데이터가 특정 분포로부터 만들어졌을(generate) 확률을 말한다. 예를 들어, X = (1, 1, 1, 1, 1)이라는 데이터가 있다고 하자. 그리고 아래와 같이 두 분포가 있다고 하자.

우리의 데이터 X는 어떤 분포를 따를 확률이 더 높을까? 당연히 왼쪽 분포를 따를 확률이 더 높을 것이다. 이런 상황에서 우리는 왼쪽 분포의 데이터 X에 대한 likelihood가 더 높다고 표현할 수 있다. 그러므로 likelihood는 다음과 같은 식으로 표현할 수 있다.

그렇다면 이 likelihood는 어떻게 계산할 수 있을까? 우리의 distribution(분포)이 θ=(μ, σ) 의 parameter를 가지고 있는 정규분포라고 가정하자. 그러면 한 개의 데이터가 이 정규분포를 따를 확률은 다음과 같이 계산할 수 있을 것이다. (그냥 정규 분포의 PDF에 x_n 값을 넣은 것이다.)

그렇다면 모든 데이터들이 독립적(independent)이라고 가정하면 다음과 같은 likelihood 식을 얻을 수 있다.
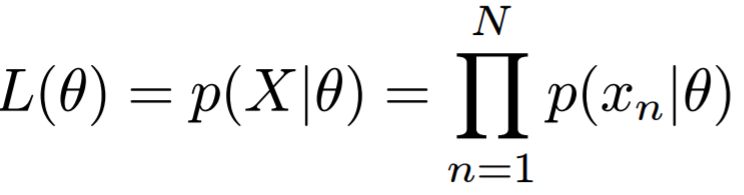
Maximum Likelihood
log likelihood
우리는 위 설명에서 likelihood의 계산식을 얻었다. 데이터 X가 θ의 parameter를 가지는 distribution을 따르려면 이 likelihood가 최대가 되는 distribution을 찾아야 할 것이다. 우리는 최댓값을 구할 때 주로 미분을 사용한다. 하지만 식이 곱셈(pi)으로 연결되어 있는 탓에 이 식에 바로 미분을 적용하기는 쉽지 않다. 그러므로 우리는 이 식에 log와 -를 취해서 그 값이 최소가 되는 값을 구함으로써 maximum likelihood를 만들어주는 값을 구한다. 이 식을 log likelihood라고 한다.

Maximum Likelihood의 계산
그러면 이제 likelihood를 최대화하는 (log likelihood를 최소화하는) θ 값을 찾을 차례이다. 이를 위해 우리는 log likelihood 식을 미분하고, 이 식이 0이 되는 값(극솟값)을 찾는다. 즉, 다음 식을 만족하는 θ 값을 찾아야 하는 것이다.

저 θ 값을 찾으면 우리는 likelihood를 최대화할 수 있다. 이의 계산 과정을 보이기 위해 정규 분포를 예로 들어서 설명하도록 하겠다. 우리의 분포가 θ=( μ, σ)의 정규분포라면 p 값은 다음과 같은 식일 것이다. (정규분포의 PDF이다.)

그러므로 우리는 이 식을 위 식에 적용시키면 다음과 같은 계산과정에 따라 최종 결과를 얻을 수 있다. (자세한 미분 계산 과정은 생략한다. 미분 과정에 대한 질문은 댓글로 가능하다.)

우리는 위 식을 0으로 만드는 parameter θ=(μ, σ)을 찾아야 한다. σ는 분모에 있기 때문에 이 값으로는 식을 0으로 만들 수 없다. 그러므로 우리는 μ 값을 다음과 같이 정의함으로써 식을 0으로 만들 수 있다.

이 평균(μ) 값을 이용해 우리는 분산(σ) 값 또한 도출해낼 수 있다.

이처럼 likelihood를 최대화하는 parameter 값을 maximum likelihood estimate라고 한다. 즉, 위 평균 값과 분산 값의 parameter가 정규분포에 대한 maximum likelihood estimate인 것이다.
이번 포스팅에서는 maxium likelihood estimation이 무엇인지에 대해 알아보았다. maximum likelihood 기법은 머신러닝에서 모수를 추정할 때 가장 자주 쓰이는 개념 중에 하나이다. 하지만 maximum likelihood는 분산을 실제보다 작게 추정하여 표본에 대하여 overfitting될 수도 있다는 한계점도 지닌다.








최근댓글