정말 오랜만에 하루에 글 두 개 ㅎㅎ 매년 100개씩 쓰는게 목푠데 올해에 과연 달성할 수 있을지 모르겠다.
알파 알고리즘 (Alpha Algorithm)은 프로세스 마이닝에서 가장 기본이 되는 process discovery 알고리즘이다.
* 이 포스팅의 이해를 위해서는 알파 알고리즘에 대한 이해가 필수적이다.
하지만 이 알파 알고리즘은 <..., a, a, a, ...>와 같이 길이가 1인 loop나 <..., a, b, a, b, a, ...>와 같이 길이가 2인 loop는 표현할 수 없다는 단점을 가진다. 이러한 알파 알고리즘의 단점을 극복하기 위해 등장한 알고리즘이 알파 + 알고리즘(alpha plus algorithm)이다. 이번 포스팅에서는 이 알파 + 알고리즘에 대해 알아볼 것이다.
length 2 loop
length-2-loop는 다음과 같은 형태의 loop를 말한다.

즉, 위 그림에서처럼 b와 c가 반복되는 형태의 loop를 말한다. 예를 들어, 이벤트 로그가 L = [<a, b, d>, <a, b, c, b, d>, <a, b, c, b, c, b, d>]와 같은 형태를 띤다면 이는 length-2-loop를 포함한 이벤트 로그라고 할 수 있을 것이다. (이를 계속 예시로 사용할 것이다.) 우리가 이 L 이벤트 로그를 알파 알고리즘을 통해 process discovery한다고 하자. 그러면 결과 페트리 넷은 다음과 같은 형태가 된다. (중간 과정은 생략한다.)
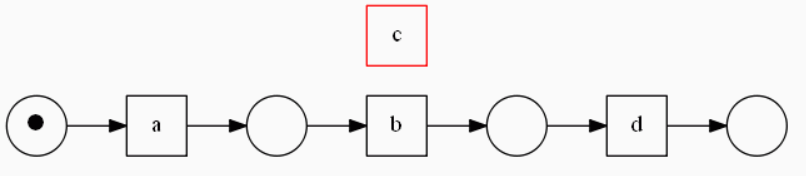
즉, length-2-loop를 발견할 수 없는 것이다. 이러한 문제를 해결하기 위해서 우리는 다음과 같이 ordering relation을 새로 정의한다.

기존의 알파 알고리즘과 어떤 차이가 있는가? 기존의 알파 알고리즘은 direct succession (>), causality (->), parallel (||), choice(#)의 네 가지 relation만 가지고 있었다. 하지만 이 length-2-loop를 찾기 위한 새로운 알파 알고리즘은 두 개의 relation을 추가한다. 이를 하나씩 풀어 쓰면 다음과 같다.
- a △ b: length-2-loop 관계를 가지는 두 액티비티를 말한다. 즉, <..., a, b, a, ...>의 형태가 trace 내에 나타나면 a △ b 관계인 것이다. 우리의 예시 이벤트 로그에서는 (b, c), (c, b)가 이에 해당된다.
- a ♢ b: <..., a, b, a, ...> 형태와 <..., b, a, b, ...> 형태가 모두 나타났을 때 이에 해당된다. 우리의 예시 이벤트 로그에서는 (b, c), (c, b)가 이에 해당된다.
- a > b: 기존의 알파 알고리즘과 같다. 이벤트 로그 내의 하나의 trace 내에서 바로 뒤에 따라오는 (directly follows) 관계의 액티비티를 말한다. 우리의 예시 이벤트로그 L에서는 (a, b), (b, c), (b, d), (c, b)가 이에 해당된다.
- a -> b: a>b이고 b>a가 아니거나 a>b이고 a ♢ b인 경우를 말한다. 우리의 예시에서는 (a, b), (b, c), (b, d), (c, b)가 이에 해당된다.
- a # b: 기존의 알파 알고리즘과 같이 서로 아무 관계도 없는 경우를 말한다. 우리의 예시에서는 (a, a), (a, c), (a, d), (b, b), (c, a), (c, c), (c, d), (d, a), (d, c), (d, d)가 이에 해당된다.
- a || b: a>b이고 b>a이며 a ♢ b가 아닌 경우를 말한다. 우리의 예시에서는 존재하지 않는다.
이제 이 ordering relation으로 표를 그리면 다음과 같다.
| a | b | c | d | |
| a | # | -> | # | # |
| b | <- | # | -> | -> |
| c | # | -> | # | # |
| d | # | <- | # | # |
이제 이에 대해서 우리가 알고 있는 알파 알고리즘을 그대로 적용하면 된다. 그러면 우리는 시작과 끝 place를 제외하고 (ac, b), (b, cd) place들을 얻게 된다. (알파 알고리즘의 자세한 연산은 생략한다.) 이를 그림으로 그리면 다음과 같다.
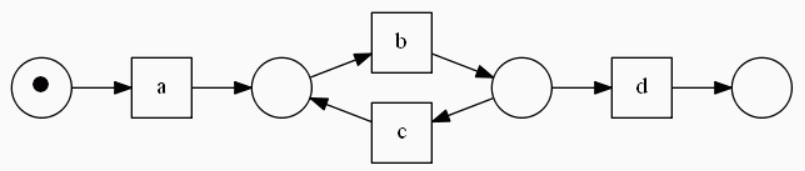
length-2-loop를 예쁘게 보여주는 페트리 넷이 도출되었다. 하지만 위 알고리즘은 하나의 치명적인 결함을 가진다. 이벤트 로그 L이 다음과 같은 페트리 넷으로부터 도출되었다고 하자.

위 페트리 넷에서 나타나는 형태 (b, c)의 loop를 length-1-loop라고 한다. 이 페트리 넷 또한 <a, b, d>, <a, b, c, b, d>와 같은 trace들을 만들 수 있다. 그러므로 우리는 우리의 이벤트 로그가 length-1-loop를 포함하지 않는다고 가정해야 위와 같은 알고리즘을 제대로 적용시킬 수 있다. 하지만 이러한 가정을 한다면 우리가 알고리즘을 적용시킬 수 있는 범위는 굉장히 한정적일 것이다. 그렇다면 length-1-loop는 어떻게 다루어야 할까?
length-1-loop
length-1-loop를 필터링하고 나서 length-2-loop를 찾는 알고리즘을 적용시키기 위해 우리는 length-1-loop를 찾는 방법을 알아내야 한다. 이는 간단하다. 이벤트 로그에서 <..., t, t, ...>와 같은 패턴이 보이면 이는 length-1-loop이다. 이 length-1-loop를 찾았다면 어떻게 해야할까? 이에 해당하는 트랜지션을 페트리 넷의 적절한 place와 연결시켜주어야 할 것이다. 이 place는 다음과 같은 방법으로 찾을 수 있다. (t가 loop에 해당하는 트랜지션이라고 가정한다.)
- t > a and a ≯ t: 이벤트 로그에서 <..., t, a, ...> 형태는 나타나지만 <..., a, t, ...> 형태는 나타나지 않는 경우이다. 이 때는 a의 input place가 t의 output place가 된다.
- t ≯ b: and b > t: 이벤트 로그에서 <..., b, t, ...> 형태는 나타나지만 <..., t, b, ...> 형태는 나타나지 않는 경우이다. 이 때는 b의 output place가 t의 input place가 된다.
예를 들어, <a, t, t, t, b>와 같은 trace가 있고, a와 b 사이에 input place가 하나 있었다고 하자. 이에 대해 위 조건을 적용시키면 다음과 같은 형태가 될 것이다.

이와 같이 length-1-loop를 처리할 수 있다.
alpha + algorithm
이제 위에서 말한 모든 것들을 종합해서 알파 + 알고리즘을 적용시킬 차례이다. 알파 + 알고리즘은 다음과 같다.
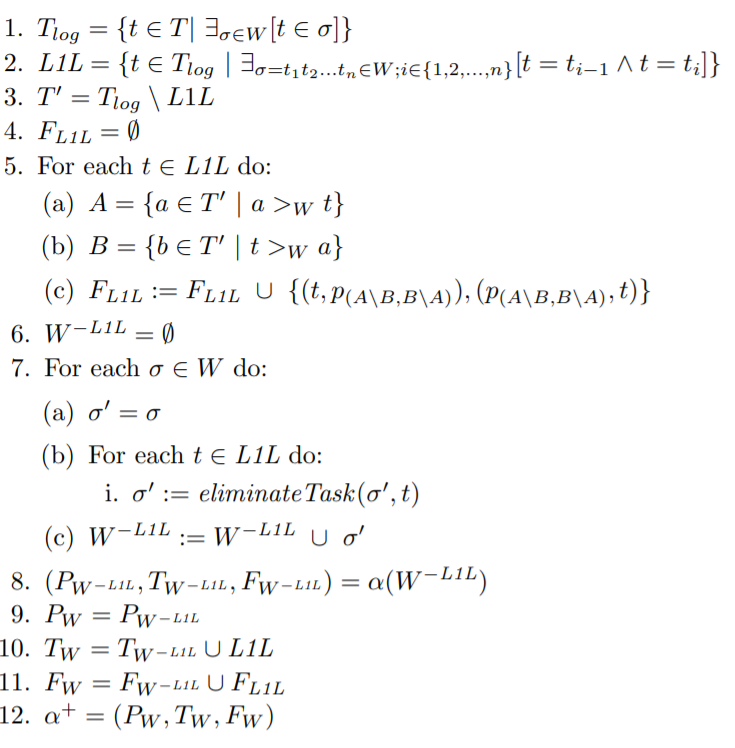
무섭게 생겼지만 이 알고리즘도 하나하나 보면 어렵지 않다.
1단계는 이벤트 로그 안의 모든 트랜지션을 찾는 과정이다. 2단계에서는 이벤트 로그에서 length-1-loop인 액티비티를 찾는다. 3단계에서는 1단계에서 찾은 모든 트랜지션에서 length-1-loop에 해당하는 트랜지션을 제거한다. 5단계에서는 우리가 위에서 length-1-loop를 처리했던 것처럼 length-1-loop를 처리한다. 그리고 7, 8단계에서 이렇게 length-1-loop를 제거한 transition들에 대해서 우리가 위에서 length-2-loop를 처리했던 것처럼 length-2-loop를 다루는 알파 알고리즘을 적용시킨다. 그리고 9, 10, 11, 12단계에서 위 두 과정에서 찾은 모든 트랜지션과 place를 종합시킨다. 이러한 알고리즘을 통해 length-1-loop와 length-2-loop를 처리할 수 있다.
이번 포스팅에서는 loop를 다룰 수 없다는 알파 알고리즘의 한계를 극복하기 위해 만들어진 알파 + 알고리즘에 대해 알아보았다. 이를 통해 좀 더 정확한 process discovery가 가능할 것이다.
References
Medeiros, A. K. Alves de, Boudewijn F. van Dongen, Wil M. P. van der Aalst and A. J. M. M. Weijters. “Process Mining : Extending the α-algorithm to Mine Short Loops.” (2004).








최근댓글