Decision Tree의 Impurity 지표 (Entropy, GINI index, GR)

 * 이번 포스팅은 Decision Tree에 대한 기본적인 이해가 있다는 것을 가정한다.

 Decision Tree는 데이터를 이용하여 tree 구조를 만드는 것을 통해 이를 분류하거나 결과값을 예측하는 분석 방법을 말한다. 이 Decision Tree를 만들 때에는, 각 node들의 복잡성, 즉 impurity가 가장 낮은 방향으로 tree가 만들어진다. 즉, 결과 노드 (leaf node) 안에서 섞여 있는 정도가 낮은 tree를 만드는 것이 목표인 것이다. 그렇다면 이 복잡성을 어떻게 측정할 수 있을까? 이번 포스팅에서는 이 Impurity 지표에는 무엇이 있는지에 대해 알아보겠다.

Entropy

 가장 기본적인 impurity 지표는 Entropy이다. Entropy는 다음 식으로 계산할 수 있다.

Entropy 계산식

예를 들어, 다음과 같은 decision tree가 있다고 하자. 

예시 decision tree

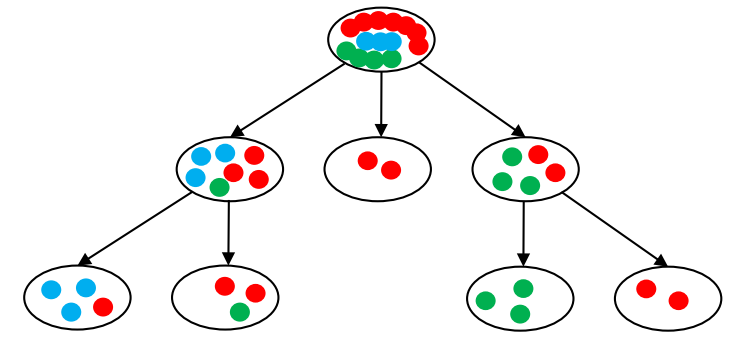
그러면 우리는 이 각각의 node들의 entropy를 다음 식과 같이 구할 수 있다.

decision tree에서 맨 위 노드

위 노드의 entropy 식. 계산하면 1.4926.

 

decision tree에서 오른쪽 위에서 두 번째 노드

위 노드의 entropy 식. 계산하면 0.9710.

GINI Index

 다음 impurity 지표는 GINI index이다. GINI index는 다음과 같은 식으로 계산할 수 있다. 

GINI index 계산식

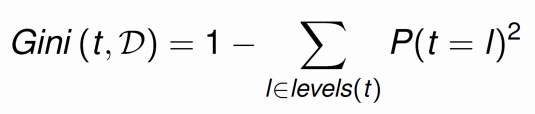
위 예시와 똑같은 node의 impurity를 GINI index를 이용해 계산해보자. 

decision tree에서 맨 위 노드

위 노드의 GINI index 식. 계산하면 0.6224.

decision tree에서 오른쪽 위에서 두 번째 노드

위 노드의 GINI index 식. 계산하면 0.52.

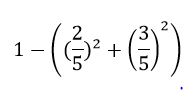
Information Gain

 위에서 살펴본 Impurity 지표들을 바탕으로 우리는 각 node들의 복잡성을 계산할 수 있다. 그리고 이 impurity를 바탕으로, (decision tree에 의해 나누기 전의 impurity - 나누어진 subset들의 impurity) 값을 통해 impurity가 얼마나 개선되었는지를 계산할 수 있고, 이를 information gain이라고 한다. 예를 들어, 우리의 예시 decision tree에서 일부분을 살펴보자.

예시 decision tree의 일부분

impurity 지표로 GINI index를 사용한다고 가정하자. 그러면 위 노드(parent node)의 GINI index는 우리가 위에서 계산했듯이 0.52가 되고, 아래 노드(child node)의 GINI index는 각각 0이므로 합하면 0이 된다. 그러므로 우리의 information gain은 0.52가 된다. 

 하지만 이러한 information gain은 한계점을 지닌다. 왜냐하면 split을 더 잘게 많이 할수록 information gain 값은 커질 수밖에 없기 때문이다. 다음 그림을 보자.

Information Gain의 한계점

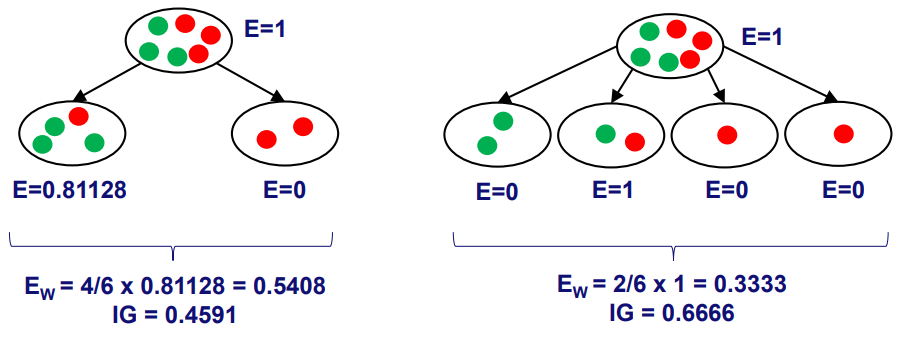
 왼쪽 decision tree는 두 개로 split을 했고, 오른쪽 decision tree는 네 개로 split을 했다. 더 많이 split을 한 오른쪽 decision tree가 각 node의 impurity가 낮기 때문에 information gain에서는 더 좋은 성능을 보인다. 하지만 오른쪽 split이 더 좋은 split이라고 말할 수 있을까? 만약 저것이 item의 개수만큼 6개로 나누어진다면 entropy가 0이 되는데 좋은 split일까? 아닐 것이다. 이를 보완하기 위해 만들어진 개념이 Information Gain Ratio이다.

Information Gain Ratio (GR)

 Information Gain Ratio(GR)은 다음 식과 같이 계산할 수 있다. 

GR의 계산식

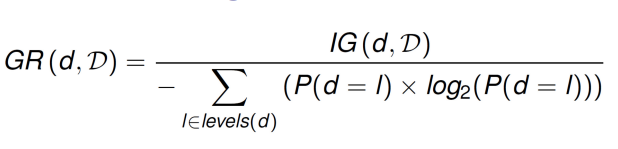
예시와 함께 의미를 살펴보자. 위에서 본 Decision tree를 다시 살펴보겠다.

위에서 본 Decision Tree

왼쪽 decision tree에서 GR의 분모값은 다음과 같이 계산할 수 있다.

또한 오른쪽 decision tree의 GR 분모값은 다음과 같이 계산할 수 있다. 

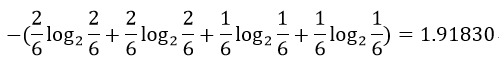
그러므로 각각의 GR 값을 계산하면 다음과 같다.

각 decision tree의 GR 값을 계산함

이를 통해 GR 값이 split이 많이 된 decision tree에 대해서 disadvantage를 주는 것을 알 수 있다. 

 

 이번 포스팅에서는 Impurity의 지표인 Entropy, GINI index와 더불어 Information Gain Ratio (GR)에 대해서도 알아보았다. 다양한 impurity 지표를 decision tree에 적용시킴과 동시에 Information Gain Ratio까지 고려함으로써 더 좋은 성능의 decision tree를 만드는 것이 가능할 것이다.

 

References

1. Course: Introduction to Data Science. Wil van der Aalst. RWTH.