K-means clustering은 클러스터의 개수를 미리 정하여 반복적으로 클러스터의 평균을 업데이트하며 가장 가까운 점들을 군집화하는 방법으로, clustering의 가장 기본이 되는 기법이다. 이번 포스팅에서는 K-means clustering이 무엇이고, 이 알고리즘의 장단점이 무엇인지에 대해 알아보겠다.
K-means clustering 알고리즘
K-means clustering은 정말 간단하게 설명될 수 있다. 우선, 다음과 같은 예시가 있다고 하자. 우리는 아래 그림의 점들을 적절하게 clustering하기를 원한다.

1. 몇 개의 덩어리로 clustering할지 정한다.
우리가 가장 먼저 해야할 일은 몇 개의 덩어리(k)로 clustering을 할 것인지 결정하는 것이다. 이 개수는 자신이 원하는 수로 아무거나 정하면 된다. 우리는 3개의 덩어리로 clustering을 해 보겠다.
2. 1에서 정한 개수만큼 중심점을 정한다.
다음으로, 1에서 정한 개수만큼 자신이 원하는 아무 값으로 중심점을 정한다. 우리의 예시에서 3개의 중심점을 아무렇게나 정하면 다음과 같다. 우리는 이 중심점을 centroid라고 부른다.

3. 각 점마다 가장 가까운 centroid를 정한다.
이제 각 점(sample)에 대해서 가장 가까운 centroid를 정한다. 이 때, 가까움, 즉 거리를 어떻게 정의하는지를 알고 싶다면 다음 글을 참고한다. 우리의 예시에서 각 점마다 가장 가까운 centroid를 매핑하면 다음과 같다. k1에 매핑된 것이 연두색, k2에 매핑된 것이 빨간색, k3에 매핑된 것이 파란색이다.
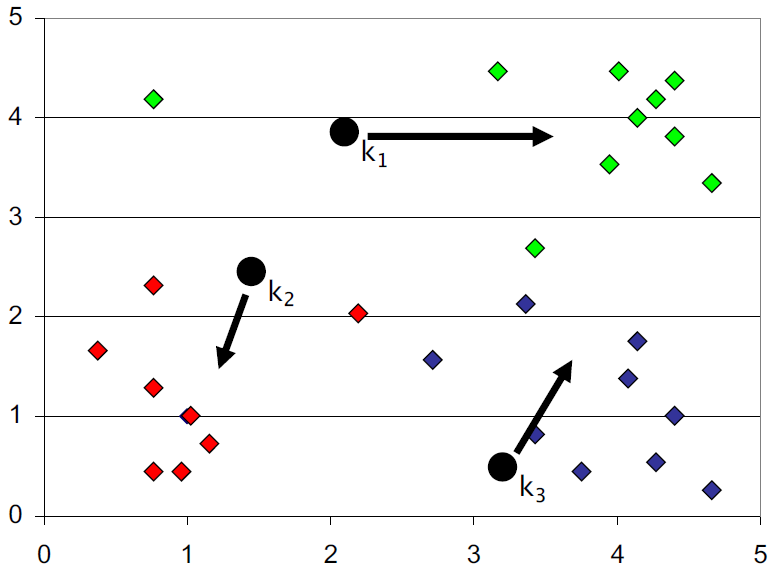
4. Centroid를 이동한다.
이제 각 매핑된 점들을 바탕으로 하여 centroid를 이동한다. 이 때, 새로 만들어지는 centroid는 같은 색으로 매핑된 점들의 평균이 된다. 그러므로 3개의 평균이 더 생기게 되는 것이다. 이렇게 k개의 평균(mean)을 바탕으로 하여 clustering을 진행하기 때문에 K-means clustering이라는 이름이 붙은 것이다. 우리의 예시에서 centroid를 이동하면 다음과 같다.

5. 3-4의 과정을 더 이상 새로 매핑되지 않을 때까지 반복한다.
이제 3의 과정을 다시한다. 즉, 새로 이동된 centroid에 대해서 각 점들이 가장 가까운 centroid를 찾는 것이다.

그 후 새로 매핑된 점들을 바탕으로 다시 centroid를 이동한다.

위의 과정을 더 이상의 이동이 없을 때까지 반복한다. 이렇게 더 이상의 이동이 없어지면, clustering이 완료되고 3개의 cluster가 생성된다.
K-means clustering의 장단점
K-means clustering의 장단점은 다음과 같다.
장점
- 쉽고 빠르게 연산이 가능하다.
- local minimum으로 수렴한다.
단점
- k 값을 임의로 정해야 하고, 처음의 centroid도 임의로 정해야 한다. 또한 처음의 centroid를 어떻게 정하느냐에 따라 cluster 결과가 민감하게 변한다.
- Outlier에 민감하다. 몇 개의 점이 굉장히 멀리 떨어져 있다면 이에 맞춰 centroid를 정하기 때문이다.
- 원(혹은 구)형(spherical)의 cluster만 찾을 수 있다. 아래 예시와 같이 cluster의 모양이 원형이 아닐 때는 정확한 결과를 도출하지 못한다.

이번 포스팅에서는 K-means Clustering에 대해 알아보았다. 가장 간단한 clustering 알고리즘인데, 이를 시작으로 여러 clustering 알고리즘들을 다 정리해봐야겠다.
* 프로세스 마이닝에서 clustering을 어떻게 활용하는지 알고 싶다면 다음 포스팅을 참고한다.
References
1. Washington University. BIO5488 lecture (2004)








최근댓글