Maximum Likelihood Estimation은 우리가 어떤 parameter를 추정할 때, likelihood 값을 최대로 하는 parameter를 찾는 과정을 말한다. 하지만 Maximum Likelihood Estimation은 우리가 기본적으로 알고 있는 데이터의 사전 지식 정보는 반영하지 못한다는 한계를 가진다. 이러한 단점을 극복하고, 우리가 데이터에 대한 정보가 있는 상황에서 posterior 값을 최대로 하는 parameter를 찾는 과정을 우리는 MAP estimation이라고 부른다. 이번 포스팅에서는 MAP estimation이 무엇인지, Maximum Likelihood Estimation과는 어떻게 다른지, 그리고 MAP estimation의 단점은 무엇인지에 대해 알아보겠다.
* 이 포스팅은 prior와 posterior에 대한 이해가 있다고 가정한다.
개념
기본 개념은 간단하다. 우리는 posterior를 베이즈 정리에 따라 다음과 같이 표현할 수 있다.
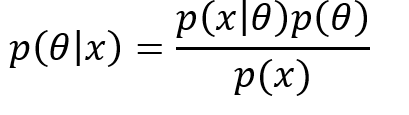
즉, 위에서 표현된 posterior를 최대로 하는 theta를 찾는 것이 우리의 목적이다. 우리는 이미 x의 분포를 알고 있다고 가정하기 때문에, (p(x)는 상수) 결국 posterior를 최대로 하는 theta를 찾는 것은 likelihood와 prior를 곱한 값을 최대로 만드는 theta를 찾는 것과 같다. 이를 식으로 표현하면 다음과 같다.

MLE와 MAP
Maximum Likelihood Estimation과 Maximum A Posterior를 말로 쉽게 풀어서 설명하면 다음과 같다. 예를 들어, 어떤 사람의 통장잔고(x)를 보고, 그 사람이 게임을 하는 사람인지 안 하는 사람인지(theta)를 판단한다고 하자.
- MLE: MLE는 게임을 하는 사람들 중 그 통장잔고가 나올 확률과 게임을 하지 않는 사람들 중 그 통장잔고가 나올 확률을 비교(likelihood)하여 둘 중 더 높은 확률로 선택하는 것을 말한다. 이 경우에는 게임을 하는 사람과 게임을 하지 않는 사람의 비율(prior)은 결정에 반영되지 않는다.
- MAP:MAP는 통장잔고가 주어졌을 때, 그것이 게임을 하는 사람의 것일 확률과 게임을 하지 않는 사람의 것일 확률을 비교(posterior)하여 둘 중 더 높은 확률로 선택하는 것을 말한다. 이 경우에는 게임을 하는 사람과 게임을 하지 않는 사람의 비율(prior)은 결정에 반영된다.
즉, 우리가 알고 있는 사전 정보인 prior의 정보를 likelihood에 곱하여 반영함으로써 더 정확한 판단을 내리는 것이 MAP estimation인 것이다.
MAP의 한계점
하지만 이러한 MAP도 여러 한계점들을 지닌다.
- Uncertainty를 계산할 수 있는 방법이 없다. 우리가 estimation을 하고 나면, 우리가 그 결과를 얼마나 신뢰할 수 있는지를 측정할 기준이 필요한데, MAP estimation에서는 이를 측정할 수 있는 명확한 기준이 없다.
- Overfitting의 우려가 있다. 우리가 Uncertainty를 측정할 수 있는 방법이 없기 때문에, 예측 정확도를 높이는 데에만 집중하다보면 분포가 overfitting될 수도 있다는 문제가 있다.
이번 포스팅에서는 MAP estimation이 무엇인지에 대해 알아보았다.
References
Machine Learning: A Probabilitstic Perspective (Adaptive Computation and Machine Learning Series) by Kevin P. Murphy (Author). Chapter 5.








최근댓글