K-nearset neighbors (KNN) 는 주어진 데이터에서 가장 가까운 데이터들의 label을 활용하여 해당 데이터의 분류를 진행하는 기법이다. 이번 포스팅에서는 대표적인 non-parametric model인 K-nearest neighbor classifier에 대해 알아보겠다.
Motivation
K-nearest neighbor classifier의 작동 원리는 정말 간단하다. 예를 들어, 다음과 같이 빨강 초록 파랑 3가지 색으로 label된 데이터가 있다고 하자.
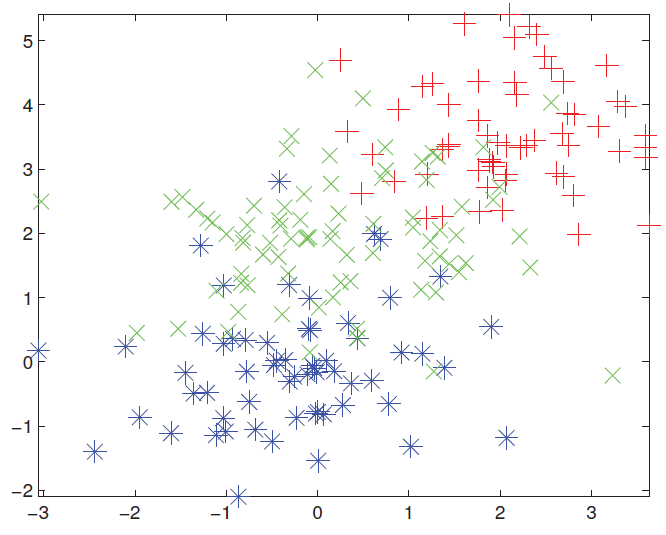
이렇게 미리 주어진 데이터가 있는데, 우리는 다음과 같은 노란 점이 빨강 초록 파랑 중 어떤 색을 가질지를 알고 싶다.

우리의 직관으로 주위에 빨강이 대부분이니까 저 노란색 점도 빨강일 것이라고 쉽게 예측할 수 있다. 이러한 단순한 직관을 이용한 것이 바로 K-nearest neighbor이다. 이름 그대로 주위에 있는 K개의 점들의 label을 보고, 가장 많은 label로 해당 input의 label을 예측하는 것이다. 예를 들어, 우리의 K가 3이라고 하자. 그러면 우리는 아래와 같은 방법으로 우리의 input의 label이 무엇일지 예측할 수 있을 것이다.

정의
* 수학이 싫으신 분들은 이 부분 스킵하셔도 좋습니다.
우리가 위해서 살펴 보았던 주위에 있는 K개의 점들의 label을 보고, 가장 많은 label로 해당 input의 label을 예측하는 것을 식으로 나타내면 다음과 같다.

즉, y라는 데이터가 c라는 label일 확률이 K개의 가장 가까운 점들 중 c라는 label을 가지는 점들의 개수 / K 값과 같다는 것이다. 즉, 우리의 K가 10이라고 할 때 K-nearest point들이 빨강이 5개, 파랑이 3개, 초록이 2개라면 해당 input이 빨강일 확률은 0.5, 파랑일 확률은 0.3, 초록일 확률은 0.2라는 것이다. 여기에서 가깝다는 것의 기준은 Euclidean distance 등의 거리로 정의될 수 있다.
Voronoi Tessellation
여기서 K 값이 1인 K-nearest neighbors를 우리는 Voronoi Tessellation이라고 부른다. 즉, 가장 가까운 곳에 있는 점의 label이 무엇인지에 따라 바로 그 점의 label을 결정하는 것이다. 그러므로 우리는 이것을 다음과 같은 그림으로 표현할 수 있고 이를 우리는 Voronoi Diagram이라고 부른다.
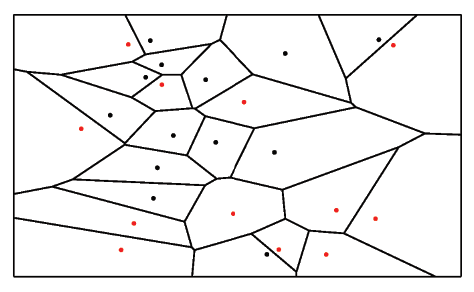
즉, 모든 공간에 대해 각 점이 가장 가깝게 선택되는 곳을 선으로 나누어 놓은 그림이다. 예를 들어, 다음과 같이 input 데이터가 들어 온다고 하자.

이 노란 점은 빨간 점이 속해 있는 분홍색 공간에 속하고, 즉 빨간 점이 가장 가까운 하나의 점이기 때문에 해당 데이터는 빨강이라고 예측할 수 있을 것이다.
이번 포스팅에서는 K-nearest neighbors와 함께 Voronoi Tessellation이 무엇인지에 대해 정의와 함께 살펴보았다. 아주 간단하고 꽤나 잘 작동하는 알고리즘이지만, dimension이 높은 데이터에 대해서는 잘 작동하지 않는다는 단점을 가지기 때문에 적절한 상황에서 잘 활용하는 것이 중요할 것이다.








최근댓글