Robust Linear Regression이란? (Laplace regression, Huber regression 장점, Huber loss)

 이번 포스팅에서는 Linear Regression과 Ridge Regression에 이어 Robust linear regression의 종류 중 하나인 Laplace Regression과 Huber Regression, 그리고 이들의 장점과 단점에 대해 알아보겠다.

* 이번 포스팅은 Linear Regression에 대한 이해가 있다고 가정한다.

Robust Linear Regression

 가장 기본적인 형태의 Linear Regression인 Least Squares는 다음과 같은 RSS(Residual Sum of Squares)를 최소화하는 w를 찾는 것을 목적으로 했다. 

Least Squares의 RSS

 하지만 위 형태와 같은 RSS를 최소화하는 모델을 만들 때 다른 데이터들과는 값이 많이 다른 아웃라이어가 데이터에 존재한다면, 이것이 모델을 왜곡할 가능성이 굉장히 클 것이다. 왜냐하면 RSS는 에러를 제곱하여 더하는 형태이기 때문이다. 예를 들어, 우리가 원하는 값이 10인데 11이라는 데이터가 5개, 9라는 데이터가 5개 있을 때는 각각의 에러를 모두 합해도 에러가 10밖에 되지 않지만, 25라는 값이 들어오면 에러를 제곱해버리기 때문에 에러가 15의 제곱인 225가 되어 식을 크게 왜곡해버릴 것이다. 즉, 기본적인 Linear Regression의 형태는 아웃라이어에 대해 민감하다는 단점을 가지는 것이다. 이러한 단점을 극복할 수 있는 식, 즉 아웃라이어에 민감하지 않은 Linear Regression을 우리는 Robust Linear Regression이라고 한다.

Laplace Regression

 Robust Linear Regression의 하나의 예는 Laplace Regression이다. Laplace Regression은 말 그대로 Laplace distribution을 우리의 likelihood로 사용하는 것이다. Laplace distribution의 PDF(Probability Density Function)는 다음과 같다.

Laplace distribution의 PDF

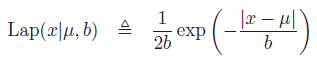
 이를 우리가 원하는 likelihood 형태로 표현하면 다음과 같이 표현할 수 있다.

Laplace regression의 likelihood

기존의 Linear Regression은 위 식에서 exp 안에 에러(y-w^Tx) 값의 제곱이 들어갔다. 하지만 저기에 제곱 대신에 절댓값이 들어감으로써 아웃라이어에 덜 민감하게 모델링이 진행되는 것이다. 이를 maximization하는 것이 우리의 목적이기 때문에, 계산의 편의를 위해 NLL(negative log likelihood)를 구한다. 이는 다음과 같다.

negative log likelihood. r = y-w^Tx

 하지만 위의 식은 linear function이 아니다. 즉, 위 식을 minimize하는 값을 찾기가 쉽지 않은 것이다. 그러므로 위 식을 linear하게 만들어주기 위해 우리는 split variable을 사용한다. 즉, r_i를 다음과 같이 정의한다.

r에 대한 split variable

그러면 우리는 우리의 식을 다음과 같은 LP(Linear Program) 형태로 바꿀 수 있다.

Laplace regeression의 NLL을 Linear Program 형태로 표현한 것

이 Linear Program을 풀면, 우리가 원하는 Laplace regression의 w 값을 구할 수 있을 것이다. (LP를 푸는 것은 이 포스팅의 범위를 넘어 생략한다. 기회가 되면 LP와 Non linear programming 포스팅도 하는 걸로 ㅎㅎ 미래의 나 화이팅~)

Huber Regression

 Robust Linear Regression의 또 다른 예는 Huber loss Function을 사용하는 Huber regression이다. 우리는 다음과 같은 loss function을 minimize하는 w를 찾는 것을 목적으로 한다.

Huber Loss Function. 이 때 r은 error(y-w^Tx) 값을 말한다.

이 Huber loss function을 자세히 보면, 에러의 절댓값이 정해진 값 델타보다 작으면 L2-error((y-w^Tx)^2), 크면 L1-error(y-w^Tx)의 형태를 가지고 있음을 알 수 있다. 즉, 에러가 작을 때는 L2-error를 취함으로써 미분이 불가능한 L1-error의 단점을 극복하고, 에러가 클 때는 L1-error를 취함으로써 아웃라이어에 민감한 L2-error의 단점을 극복하는 것이다. (위 식에서 2를 나눈 것이나 아래 식에서 델타^2/2를 나누는 것 등은 Huber loss function을 연속이고 미분가능하게 만들기 위해서이다.)

L2, L1, Huber loss function

위에서도 언급했듯이 Huber function은 모든 구간에서 미분가능하고 연속이기 때문에 LP를 푸는 것이 아닌 Smooth optimization method를 사용하는 것이 가능해지고, 이에 따라 optimizing의 속도가 굉장히 빨라진다는 장점을 가진다. 

 이번 포스팅에서는 Robust linear regression 중에서도 Lapalce regression과 Huber regression에 대해 알아보았다. 머피 책 보면서 쓰니까 블로그 너무 산수산수한 것.. 이제 7단원인데 언제 다 보져

References

Machine Learning: A Probabilistic Perspective (Adaptive computation and Machine Learning Series) by Kevin P. Murphy (Author). Chapter 7.