Probit regression은 probit function이라고도 불리는 표준정규분포의 cdf를 활용하는 classification 방법으로, logistic regression과 비슷하게 작동하지만 미분했을 때 gradient를 정규분포를 활용하여 간단하게 표현할 수 있다는 장점을 가진다. 이번 글에서는 probit regression이 무엇인지와 함께, probit regression에 MLE를 적용하는 방법에 대해 알아보겠다.
정의
Probit function
우선, probit regression에 대해 알아보기 전에 probit function이 무엇인지에 대해 알아보겠다. Probit function은 앞서 언급한 것처럼 표준정규분포의 cdf를 말한다. 이는 아래와 같이 정의된다.

이러한 probit function은 다음 그림과 같이 sigmoid function과 비슷한 형태를 가진다.

Probit function의 가장 큰 특징은 $\Phi(x)+\Phi(-x)=1$을 만족한다는 점이다. 이는 아래와 같이 증명할 수 있다.
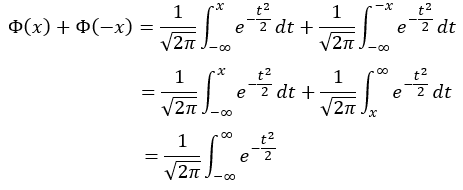
위 증명에서, 첫 번째 줄과 두 번째 줄이 같은 이유는, $e^{-t^2/2}$가 $x=0$에 대해 대칭인 함수이기 때문에 $-x$에서나 $x$에서나 값이 같기 때문이다.
Probit regression
Probit regression은 위에서 설명한 probit function을 활용한 classficiation model이다. 우리는 logistic regression을 다음과 같은 형태로 사용하였다.

이 때, sigmoid 함수 부분(sigm)은 $[-\inf, \inf]$를 $[0,1]$로 매핑하는 어떤 종류의 $g^{-1}$ 함수로 대체 가능하다. 우리는 이 sigmoid 부분을 다양한 형태로 대체하여 다양한 classfication 모델들을 만들 수 있다.

이 중 하나가 $g^{-1}$ 함수로 probit function을 사용한 probit regression이다.
Probit regression과 MLE
Probit regression은 앞서 설명한 것처럼 미분했을 때 gradient를 정규분포를 활용하여 간단하게 표현할 수 있다는 장점을 가진다. 이는 maximum likelihood estimation을 활용해서 parameter를 추정하기가 쉽다는 것이다. Probit regression에서 MLE가 어떻게 적용되는지를 살펴보기 위해 우선 다음과 같이 $\mu_i$와 예측하는 label을 정의한다.

이를 통해 우리는 $x_i$에서의 log likelihood의 미분값을 다음과 같이 도출할 수 있다.

위 식에서 첫 번째 구성요소인 $d\mu_i / dw$는 $x_i$가 된다. 다음으로, 두 번째 구성 요소인 log likelihood의 $\mu_i$에 대한 미분에 대해 설명하겠다. 우선, 우리의 모델의 likelihood는 다음과 같은 식으로 표현할 수 있다.

이 때, 우리는 probit function의 특징인 $\Phi(x)+\Phi(-x)=1$을 활용하여 label이 -1일 때의 likelihood를 다음과 같이 표현할 수 있다.

그러므로 우리는 likelihood를 아래와 같은 식으로 다시 표현할 수 있다.

그리고 이를 $\mu_i$에 대해서 미분하면, 다음과 같은 식이 도출된다. 이 때, 마지막 등호가 성립하는 이유는 표준정규분포가 x=0에 대해서 대칭인 함수이기 때문에 -1 혹은 1을 곱하는 것에 의해 값이 변하지 않기 때문이다.

결론적으로, 우리는 다음과 같은 log likelihood의 미분값을 얻을 수 있다.

이를 활용해서 우리는 Hessian (2차 미분) 값도 아래와 같이 얻을 수 있다. 이의 도출 과정은 생략한다.

이번 글에서 우리는 probit regerssion이 무엇인지와 함께 probit regression에 대해 maximum likelihood estimation을 어떻게 적용할 수 있는지에 대해 알아보았다. 백수일 때에도 주에 2개 글 쓰는 것이 쉽지 않은데 2019년의 나는 어떻게 출근하면서 주에 2개 쓴 건지 좀 의문스럽다.. 당신 대단해
References
1. Machine Learning: A Probabilitstic Perspective (Adaptive Computation and Machine Learning Series) by Kevin P. Murphy (Author).








최근댓글