우리는 어떤 데이터에 대한 parameter를 추정하고 싶을 때, 주로 Maximum Likelihood Estimation 혹은 MAP Estimation을 사용한다. 하지만 이외에도 MOM(Method of Moments), ERM(Empirical Risk Minimization) 등 parameter를 추정하는데에 쓰이는 다양한 방법들이 존재한다. 이번 포스팅에서는 그 중에서도 MLE를 일반화하여 표현한 방법인 Emprical Risk Minimization이 무엇인지에 대해 알아보겠다.
정의
Empirical Risk Minimization은 loss function이 어떤 형태이든 적용할 수 있는 방법으로, 이 방법에서는 loss function을 아래 식과 같이 정의한다.
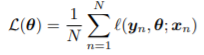
위 식에서 l(y_n, theta;x_n)은 x_n과 theta를 기반으로 추정한 값과 y_n과의 loss를 의미한다. 즉, 위 식의 의미는 모든 N개의 input data x_n에 대해서 해당하는 y_n을 추정하여 얻은 loss들의 평균값이라고 할 수 있다.
예시
예를 들어, 우리가 multi-class classification 문제를 푼다고 하자. 그러면 우리는 우리의 loss function을 아래와 같이 정의할 수 있다.
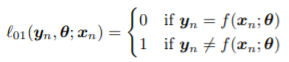
즉, label이 맞으면 loss가 0이고, label이 틀리면 loss가 1인 것이다. 이를 위 ERM의 정의 식에 넣으면 우리의 empirical risk는 아래 식과 같이 표현될 것이다.
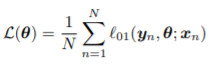
위 식을 들여다보면, N개의 classification 문제 중 제대로 classify하지 못한 것의 비율, 즉 misclassification rate를 나타내고 있음을 알 수 있다. 즉, multi-class classification 문제에서의 Empirical Risk는 misclassification rate와 같고, 결국 이를 최소화하는 것이 misclassification을 최소화하는 것과 동일하므로 ERM이 합리적인 parameter estimation 방법인 것이다.
또 다른 예시로, 우리가 binary classification 문제를 푼다고 하자.그러면 우리는 우리의 loss function을 아래와 같이 정의할 수 있다.

위 식에서 y_tilde는 -1과 1 중 하나의 값을 갖는 true label, y_hat은 -1과 1 중 하나의 값을 갖는 predicted label이다. 즉, 두 값을 곱해 0 미만이라는 의미는 예측이 틀렸다는 것을 의미하고, 이렇게 예측이 틀렸을 때 loss 값이 1이 된다. 이를 위 ERM의 정의 식에 넣으면 우리의 empirical risk는 아래 식과 같이 표현될 것이다.

이 또한 위에서 살펴본 multi-class classification 문제와 같이, misclassification rate를 나타냄을 알 수 있다. 즉, 이 경우에도 ERM이 합리적인 parameter estimation 방법인 것이다.
이번 포스팅에서는 parameter estimation 방법 중 하나인 ERM이 무엇인지에 대해 알아보았다. MLE를 general한 방법으로 표현한 ERM 또한 parameter estimation에 적절하게 활용하면 좋을 것이다.
References
1. Probabilistic Machine Learning: An Introduction by Kevin Patrick Murphy. MIT Press, February 2022.








최근댓글