Forward KL Divergence과 Reverse KL Divergence 설명 (Inclusive KL과 exclusive KL)

 이번 포스팅에서는 저번 KL divergence 글에 이어, forward KL과 reverse KL이 무엇인지에 대해 설명하겠다. 

Forward KL

 Forward KL(inclusive KL)은 아래와 같이 정의한다. 이는 기존에 우리가 알던 KL divergence의 형태와 같다.

forward KL의 정의

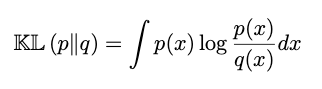
 이 Forward KL을 최소화하는 q를 찾는 과정을 우리는 M-projection 혹은 moment projection이라고 부른다. 그렇다면 우리는 이 forward KL을 어떻게 해석할 수 있을까? 이를 해석하기 위해 전체 x 값을 p(x)=0인 구간과 p(x)>0인 구간으로 분류한다.

p(x)=0

 p(x)가 0인 구간에 대해서 우리는 KL divergence를 고려할 필요가 없다. 왜냐하면, KL divergence는 p(x)에 log(p(x))/log(q(x))를 곱한 값이기 때문에, p(x)=0을 만족하면 해당 구간에서는 KL divergence 값이 0이 되기 때문이다. 

p(x)>0

 p(x)가 0 초과인 구간에 대해서는, p(x)/q(x) 값이 클수록 KL divergence가 커지고, p(x)/q(x) 값이 작을수록 KL divergence 값이 작아질 것이다. 그러므로 우리는 p(x)/q(x) 값을 최소화하는 것을 목적으로 해야 한다. 이 때, p(x)>0을 만족하지만 q(x) 값이 0이 되는 구간이 있으면 아래와 같은 그림을 만족할 것이다.

p(x)>0인 구간에 대해 q(x)=0인 구간이 존재하는 경우

 이렇게 q(x)=0이 되어버리면 p(x)/q(x) 값이 매우 커지게 되고, 결론적으로 KL divergence를 최소화할 수 없게 될 것이다. 그러므로 우리는 아래 그림과 같이 p(x)>0인 구간에 대해 q(x)>0을 만족하는 q(x)가 KL divergence를 최소화하는 q(x)라고 표현할 수 있을 것이다. 

p(x)>0인 구간에 대해 모두 q(x)>0인 경우

 그러므로, Forward KL divergence가 최소화되려면 q(x)가 p(x)>0인 구간을 모두 'cover'해야 한다.

Reverse KL

 Reverse KL(exclusive KL)은 아래와 같이 정의한다. 이는 기존에 우리가 알던 KL divergence의 형태에서 p와 q의 위치를 바꾼 형태이다.

reverse KL의 정의

 이 Reverse KL을 최소화하는 q를 찾는 과정을 우리는 I-projection 혹은 information projection이라고 부른다. 이 reverse KL을 최소화하기 위해서는, 위에서 forward KL을 찾을 때와 q와 p만 바꾸어서 생각하면 될 것이다. 즉, Reverse KL divergence가 최소화되려면, p(x)가 q(x)>0인 구간을 모두 'cover'해야 한다. 

 이러한 Forward KL과 Reverse KL을 하나의 그림으로 나타내면 아래와 같다.

파란색이 true distribution p. 붉은 색이 추정 distribution인 q. (a)가 forward KL을 최소화하는 q, (b), (c)가 reverse KL을 최소화하는 q이다.

 이번 포스팅에서는 forward KL과 reverse KL이 무엇인지에 대해 알아보았다. KL(p|q)와 KL(q|p)가 어떻게 다르고, 이를 최소화하는 q가 어떤 차이를 가지고 있는지를 이해하는 데에 도움이 될 것이다.

 

References

1. Probabilistic Machine Learning: An Introduction by Kevin Patrick Murphy. MIT Press, February 2022.

2. Agustinus Kristiadi's Blog. KL Divergence: Forward vs Reverse?