Node degree와 Node centrality 설명 (betweenness centrality, closeness centrality, eigenvector centrality)

 이번 포스팅에서는 노드에 연결된 엣지 수의 합을 의미하는 node degree, 노드의 중요도를 의미하는 node centrality가 무엇인지에 대해 알아보겠다.

Node degree

 Node degree란, 노드에 연결된 엣지 수의 합을 말한다. 즉, 노드가 몇 개의 이웃(neighbor)을 가지는지를 표현한 것이라고 할 수 있다. 이를 식으로 표현하면 아래와 같다. 

node degree의 정의. 위 식에서 A는 adjacency matrix를 말한다.

  예를 들어, 아래와 같이 생긴 그래프가 있다고 하자. 이 예시 그래프에서 노드 A의 node degree는 C 하나의 노드만 연결되어 있기 때문에 1, 노드 D의 node degree는 B, C, E, H 네 개의 노드가 연결되어 있기 때문에 4가 될 것이다.

node degree 예시 그래프

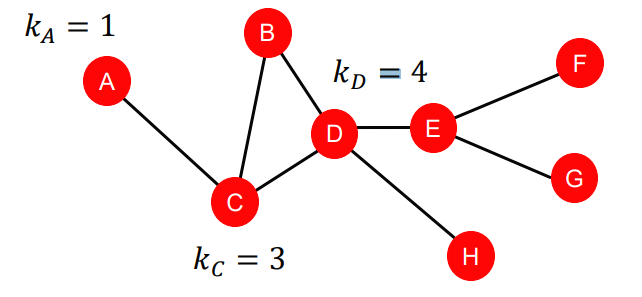
 Node degree는 가장 기본이 되는 graph statistics이기 때문에, 전통적인 머신러닝 방법을 이용해서 node-level의 특성을 예측하는 데에 기본적인 feature로 많이 사용되었다.

Node centrality

 Node centrality는 node가 그래프 내에서 얼마나 중요한지(importance)를 나타내는 measure이다. node centrality는 계산하는 방법이 하나로 정해져 있는 것이 아니라, 다양한 방법들이 존재한다. 그 중 몇 개의 예시를 소개하도록 하겠다. 

Betweeness centrality

 Betweeness centrality는 어떤 다른 두 노드 간의 shortest path 위에 해당 노드가 얼마나 자주 있는지를 표현하는 measure이다. 즉, betweeness centrality는 다른 노드들의 shortest path 위에 노드가 자주 있으면 중요한 노드라고 생각하는 것이다. 그러므로 이를 계산하는 식은 다음과 같다.

betweeness centrality의 계산식

다음과 같은 예시 그래프가 있다고 하자.

betweeness centrality 예시

이 그래프에서 노드 C의 betweeness centrality는 얼마일까? A-B로 가는 shortest path인 A-C-B, A-D로 가는 shortest path인 A-C-D, A-E로 가는 shortest path인 A-C-D-E 이렇게 3개의 shortest path에 속하기 때문에 3이 된다. (노드쌍들에 대해 다른 shortest path가 존재하지 않는다.)

Closeness centrality

 Closeness centrality는 해당 노드와 다른 모든 노드들 사이의 shortest path의 길이를 표현하는 measure이다. 즉, closeness centrality는 해당 노드가 다른 노드들에 가는 shortest path 길이가 짧으면 중요한 노드라고 생각하는 것이다. 그러므로 이를 계산하는 식은 다음과 같다.

closeness centrality의 계산식

 다시 위의 예시 그래프를 살펴보자.

closeness centrality 예시

 이 그래프에서 노드 A의 closeness centrality는 얼마일까? B로 가는 shortest path A-C-B, C로 가는 shortest path A-C, D로 가는 shortest path A-C-D, E로 가는 shortest path A-C-D-E 이렇게 네 개의 shortest path의 길이 합이 8이기 때문에 1/8이 될 것이다. 

Eigenvector centrality

 Eigenvector centrality는 이웃한 노드들의 중요도를 표현하는 measure이다. 즉, eigenvector centrality는 해당 노드의 주위에 있는 노드들이 중요한 노드이면 중요한 노드라고 생각하는 것이다. 그러므로 이를 계산하는 식은 다음과 같다.

eigenvector centrality의 계산식. lambda는 상수.

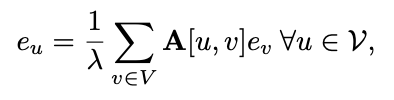
 위 식에서 A는 adjacency matrix이다. 위의 식의 답이 되는 c를 구하기 위해서, 우리는 위 식을 아래 형태로 표현할 수 있다.  

eigenvector centrality의 계산식 2

e는 centrality vector(각 node의 centrality 값을 vector로 표현)이다. 그러므로 위 식의 답이 되는 e가 결국 eigenvector centrality의 답이 될 것이다. 그런데 이 형태는, 선형대수에서 많이 보던 eigenvector / eigenvalue의 정의와 같다. 결론적으로, adjacency matrix의 eigenvector가 centrality vector가 되는 것이다.

 eigenvector centrality는 power iteration을 사용하면 아래와 같은 식을 이용해서도 계산이 가능하다. 

eigenvector centrality의 계산식 3

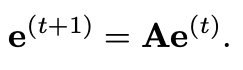
우리가 initial vector(t=0일 때 e의 vector)를 (1,1,...,1)^T로 놓으면, t=1일 때의 e는 node degree가 된다. 이를 일반화하면, 1 이상의 t에 대해 e는 길이가 t인 path가 각 노드를 방문할 빈도가 된다. 그러므로 이를 무한히 반복하여, 우리는 eigenvector centrality를 무한한 길이의 random walk에서 각 노드가 방문될 likelihood로 생각할 수 있다. 

 이번 포스팅에서 우리는 가장 기본적인 node feature인 node degree와 node centrality에 대해서 알아보았다. 다음 포스팅에서는 이외의 node feature인 clustering coefficient, graphlet 등에 대해서도 알아보겠다. 

References

1. Hamilton. William L., Graph Representation Learning. 

2. Jure Leskovec. CS224W: Machine Learning with Graphs.