Clustering Coefficient 설명 (그래프의 clustering coefficient 계산)

 이번 글에서는 node degree, node centrality에 이어 또다른 node feature인, 해당 노드에 이웃하는 노드들이 얼마나 잘 연결되어 있는지를 표현하는 지표인 clustering coefficient가 무엇인지에 대해 설명하겠다. 

정의

 Clustering coefficient는 해당 노드에 이웃하는 노드들이 얼마나 잘 연결되어 있는지를 측정하는 measure이다. 이의 정의는 아래와 같다.

clustering coefficient의 계산식

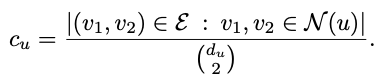
 위 식에서 d_u는 노드 u의 degree를 뜻하고, N(u)는 노드 u의 이웃 노드를 뜻한다. 그러므로 분모는 노드 u의 이웃 노드들끼리의 노드쌍의 경우의 수를 의미하고, 분자는 그 중 연결된 엣지의 수를 의미한다. 즉, clustering coefficient가 1이면 모든 이웃 노드들이 서로 연결되어 있는 것이고, clustering coefficient가 0이면 모든 이웃 노드들이 서로 연결되어 있지 않은 것이다. 

예시

 Clustering coefficient를 좀 더 직관적으로 이해하기 위한 예시에 대해 알아보겠다. 아래 그래프가 있다고 하자.

예시 그래프

 위 예시 그래프의 clustering coefficient는 얼마가 될까? 노드 v의 degree가 4이기 때문에 분모는 6(4C2)이 될 것이고, 분자는 v에 연결된 엣지를 제외한 모든 엣지가 될 것이므로 3이 될 것이다. 그러므로 clustering coefficient는 0.5이다. 그렇다면 같은 노드를 가지고 있다고 할 때 clustering coefficient가 0인 그래프는 어떤 형태일까? 아래와 같은 형태가 될 것이다.

clustering coefficient=0 그래프

이와 반대로, clustering coefficient가 1인 그래프는 어떤 형태일까? 아래와 같은 형태가 될 것이다.

clustering coefficient=1 그래프

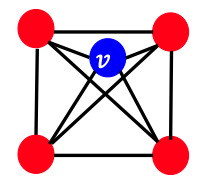
 위 예시들을 통해서 알 수 있듯이, clustering coefficient는 결국 노드를 포함하고 있는 삼각형(closed triangle)의 개수가 몇 개인지를 표현하는 지표가 되기도 한다. 

 node centrality에 다양한 종류가 있었던 것처럼 clustering coefficient에도 다양한 종류가 있다. 또한 clustering coefficient는 실제 데이터를 반영한 social network에서는 random하게 엣지를 만든 네트워크보다 훨씬 높은 값이 나타난다.

 이번 포스팅에서는 clustering coefficient의 정의와 함께 이를 어떻게 계산할 수 있는지를 예시를 통해 알아보았다. 다음 포스팅에서는 clustering coefficient를 좀 더 일반화한 node feature인 graphlet에 대해 알아보겠다. 

 

References

1. Hamilton. William L., Graph Representation Learning. 

2. Jure Leskovec. CS224W: Machine Learning with Graphs.