Graph Laplacian은 Adjacency matrix 를 다양한 방법으로 변형하여 그래프를 표현할 수 있게 한 행렬들을 말한다. 이번 글에서는 이 Graph Laplacian의 종류 중 하나인 unnormalized Laplacian, normalized Laplacian의 정의와 특성들에 대해 알아보겠다.
Unnormalized Laplacian
Laplacian matrix 중 가장 기본이 되는 matrix가 unnormalized Laplacian이다. 이는 다음과 같이 정의한다.
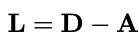
위 식에서 D는 degree matrix, A는 adjacency matrix이다. 그러므로 unnormalized Laplacian matrix의 각 성분(L[i,j])은, (self-loop가 없는 그래프 가정) i=j일 때 노드 i의 degree, i!=j이고 i와 j가 연결되어 있으면 -1, 그렇지 않으면 0이 된다.
특성
unnormalized Laplacian은 다음과 같은 특성을 가진다.
- symmetric matrix이다. (L = L^T)
- positive semi-definite matrix이다.
- 모든 vector x(dimension: 노드의 크기)에 대해 다음과 같은 특성을 지닌다.

위 2, 3 특성의 증명은 아래와 같다. (증명은 생략해도 좋다.)




4. 노드의 개수만큼의 non-negative eigenvalue들을 가진다.

Normalized Laplacian
unnormalized Laplacian을 여러 형태로 normalize하기도 한다.
Symmetric normalized Laplacian
첫 번째 normalized Laplacian은 symmetric normalized Laplacian이다. 이는 다음과 같이 정의한다.

이 식에 L의 정의를 반영하면, 위 식은 다음과 같이 다시 표현할 수 있다.

그러므로 symmetric normalized Laplacian의 각 성분(L[i,j])은, i=j일 때 1, i!=j이고 i와 j가 연결되어 있으면 -1/root(degree of i * degree of j), 아니면 0이 된다. 즉, unnormalized Laplacian을 노드의 degree로 normalize한 행렬이 되는 것이다. Symmetric normalized Laplacian은 그 이름과 같이 symmetric한 특성을 가진다.
Random walk Laplacian
두 번째 normalized Laplacian은 random walk Laplacian이다. 이는 다음과 같이 정의한다.

이 식에 L의 정의를 반영하면, 위 식은 다음과 같이 다시 표현할 수 있다.

그러므로 random walk Laplacian의 각 성분(L[i,j])은, i=j일 때 1, i!=j이고 i와 j가 연결되어 있으면 =1/degree of i, 아니면 0이 된다. 이 matrix는 symmetric하지는 않다.
이번 글에서는 그래프의 특성을 표현해줄 수 있는 matrix 중 하나인 Graph Laplacian Matrix에 대해 알아보았다.
References
1. Hamilton. William L., Graph Representation Learning.








최근댓글