local neighborhood를 활용한 measure들은, 두 노드가 공통된 이웃을 가지고 있지 않는 상황에서는 두 노드 간의 관계에 대해 추론하기 힘들다. 그러므로 이번 글에서는, 이러한 한계점을 해결하기 위해 도출된 개념인 그래프 전체를 고려하여 두 노드 간의 관계를 표현하는 Katz index에 대해 알아보고, 이와 함께 Adjacency matrix가 무엇이고 특성이 무엇인지에 대해 알아보겠다.

정의
Katz index는, 두 노드 사이의 모든 길이의 path의 빈도를 의미한다. 즉, 수학적으로 정의하면 아래와 같이 정의할 수 있다.

위 식에서 i는 두 노드 사이의 path의 길이를 의미하고, beta값은 긴 path에 대해 얼마나 weight를 줄 것인지를 결정한다. 예를 들어, beta가 1이라면 path의 길이에 상관 없이 모든 빈도를 더하고, beta가 1보다 작다면 짧은 path에 더 큰 weight를 주고, beta가 1보다 크다면 긴 path에 더 큰 weight를 주는 식이다. 그리고 A는 adjacency matrix를 의미한다. 여기서 그래프를 표현하는 가장 기본이 되는 matrix인 adjacency matrix에 대해 간단히 설명하고, 그것의 특성에 대해 알아보겠다.
Adjacency matrix
Adajacency matrix는 각 노드의 연결관계를 표현하는 행렬이다. 두 노드가 연결되어 있다면 1, 연결되어 있지 않다면 0의 값을 가진다. 예를 들어 다음과 같은 그래프가 있다고 하자.

이 그래프의 Adjacency matrix는 무엇일까? 노드 (1,2), (1,4), (2,4), (3,4)가 연결되어 있기 때문에 답은 아래와 같을 것이다.
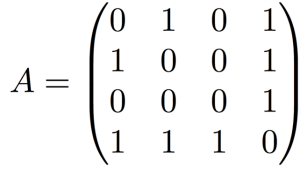
만약 우리가 Adjacency matrix를 활용해서 노드 u로부터 노드 v로 가는 length 1의 path의 개수를 찾는다면 어떻게 해야할까? 간단하다. Adjancency matrix의 성분 (u,v)를 보면 된다. 예를 들어, 위 예시 A의 (1,3) 성분이 0이기 때문에 1에서 3으로 가는 length 1의 path는 존재하지 않는 것이다.
그렇다면 만약 우리가 Adjacency matrix를 활용해서 노드 u로부터 노드 v로 가는 length 2의 path의 개수를 찾는다면 어떻게 해야할까? 우선 우리는 u의 이웃으로부터 v로 가는 길이 1의 path가 무엇이 있는지를 확인해야할 것이다. 그리고 이들의 개수를 모두 합하면, 노드 u로부터 노드 v로 가는 length 2의 path 개수를 구할 수 있다. 예를 들어, 노드 1로부터 2로 가는 length 2의 path 개수를 구한다고 하자. 그럼 우리는 다음과 같은 식을 통해 이를 계산할 수 있다.

파란 네모는 노드 1의 neighbor, 초록 네모는 이 neighbor로부터 node 2로 가는 length 2의 path를 의미한다. 그리고 이를 곱한 값이 빨간 네모가 되는 것이고, 이는 A^2의 (1,2) 성분이 된다. 이를 일반화하면, A^n은 length가 n인 path의 개수를 표현하는 matrix가 되는 것이다.
그럼 다시 Katz index의 정의로 돌아가보자.

위 정의가 두 노드 사이의 모든 길이의 path의 빈도를 의미한다는 것을 이제 이해할 수 있다.
계산
그럼 이제 저 정의에 따라 Katz index를 계산하려면 어떻게 해야할까? (아~주 약간의 선형대수가 필요하다.) 이는 아래 식과 같다.

이는 아래 정리에 의해 증명할 수 있다. (아래 정리의 증명은 생략한다.)

정리 1의 X 자리에 betaA를 넣으면, 우리가 원하는 Katz index 식에 i=0일 때의 값을 더한 것이 된다. betaA 값은 i=0일 때 identity matrix이므로, 이를 빼주면 우리가 원하는 Katz index가 된다.
이번 글에서는 Katz index가 무엇인지와 함께 이의 계산식의 증명, 그리고 Adjacency matrix의 특성에 대해 알아보았다. 초반이라 이렇게 해서 언제 GNN이 나오나 싶은데.. 차근차근.. 해야지..
References
1. Hamilton. William L., Graph Representation Learning.
2. Jure Leskovec. CS224W: Machine Learning with Graphs.








최근댓글