Line serach는 convex optimization에서 learning rate의 값을 정하는 방법으로, 우리가 최소화하고 싶어하는 함숫값이 가장 작아지는 방향으로 learning rate를 정하는 것을 말한다. 적절한 learning rate를 정하는 것은 이번 글에서는 line search, 그 중에서도 exact line search와 backtracking line search가 무엇인지에 대해 알아보겠다.
정의
Line search는 앞서 말했듯이 convex optimization에서 learning rate의 값을 정하는 방법이다. Learning rate가 너무 크면 우리가 최소화하려는 값이 수렴할 수 없고, 너무 작으면 수렴하는데에 굉장히 오랜 시간이 걸리기 때문에 적절한 learning rate를 찾는 것은 중요한 일이다. 그러므로 우리는 이 적절한 learning rate를 찾기 위해서 우리가 최소화하고 싶어하는 함숫값이 가장 작아지는 방향으로 learning rate를 정하게 되고, 이를 line search라고 한다.
Exact line search
line search의 가장 기본이 되는 예시는 exact line search이다. 우리가 최소화하고 싶은 함수를 $f$, 구하고 싶은 learning rate를 $\eta$라고 할 때, 우리는 $\eta$를 다음과 같은 식을 minimize하는 값으로 결정한다. 이를 식으로 나타내면 아래와 같다.

이를 다시 말하면, 현재의 step에서 gradient 방향으로 learning rate만큼 이동했을 때 함숫값이 가장 작아지는 learning rate를 현재 단계의 learning rate로 결정하는 것이다. 예를 들어, 다음과 같은 함수가 있다고 하자.

위 함수에서, 우리가 (2,4)에서의 최적의 learnig rate를 exact line search를 통해 찾는다고 하자. 그러면 우리는 다음과 같은 식을 통해서 learning rate를 찾을 것이다.

그러면 우리는 위 식을 통해 learning rate 1/2를 도출할 수 있다. (위 식을 \eta에 대해 미분하면 된다.) 이를 대입하면, 다음 step의 위치는 (0,0)이 될 것이고, 우리의 minimization이 끝났음을 확인할 수 있다. 하지만 이러한 exact line search 방식은 각 step에서 항상 arg min 값을 구해야하기 때문에 효율적이지 못해서 실제로는 잘 사용되지 않는다.
Backtracking line search
Exact line serach의 단점을 극복하기 위해 등장한 개념이 backtracking line search이다. Backtracking line search는 exact line search와는 달리 하나의 step을 가 보고, 해당 step에서 너무 많이 이동했으면 learning rate를 줄여서 다시 이동하는 방식으로 적절한 learning rate를 찾는 것이다. 이의 알고리즘은 다음과 같다.
1. parameter $\alpha$를 0과 0.5 사이의 값, $\beta$를 0과 1 사이의 값으로 정한다. 이 때, $\alpha$는
2. learning rate $\eta$를 1로 초기화한다.
3. 만약 아래 조건을 만족하면, $\eta$를 $\beta \eta$로 변경하여 해당 조건이 불만족될 때까지 반복한다.
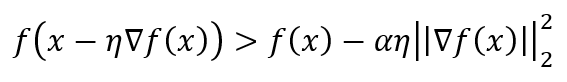
4. 해당 조건이 불만족되면, 최종 $\eta$를 learning rate로 정하여 이동하고, 종료 조건이 만족되지 않으면 2로 돌아가 반복한다.
이를 그림으로 나타내면 좀 더 이해하기가 쉽다.

위 그림에서, 붉은 점선은 현재의 위치 x에서 접선 방향으로 한 스텝 이동한 것이고, 초록 점선은 접선 방향에 $\alpha$를 곱한 방향으로 한 step 이동한 것이다. 붉은 점선을 기준으로 이동을 하게 되면 붉은 점선은 항상 우리가 최소화하기를 원하는 함수보다 항상 아래에 있기 때문에 어떤 것이 적절한 learning rate인지 구하기가 쉽지 않다. 그렇기 때문에 backtracking line search에서는 초록색 점선을 따라 한 스텝 이동한 함수보다 초록 점선이 더 클 때의 learning rate가 적절하다고 판단하여 해당 learning rate를 선택해서 사용한다. 그 결과, 우리는 위 그림에서의 노란 박스 안에서만 값을 이동시킬 수 있게 되고, 이를 반복하여 최솟값을 찾을 수 잇는 것이다.
이번 글에서는 적절한 learning rate를 찾는 방법인 line search, 그 중에서도 exact line search와 backtracking line search에 대해 알아보았다.
References
1. Machine Learning: A Probabilistic Perspective (Adaptive Computation and Machine Learning Series) by Kevin P. Murphy (Author).








최근댓글