Gradient descent (Steepest descent)는 가장 기본적인 optimization 방법론 중 하나로, 어떤 함수를 gradient의 반대 방향으로 반복적으로 이동시키면서 함수의 minimum을 찾아나가는 알고리즘이다. 이번 글에서는 gradient descent 알고리즘이 무엇이고, 이것이 어떻게 minimum을 찾아나가는지에 대해서 알아보겠다.
정의
우리가 어떤 함수 $F(x)$의 mimimum을 찾고 싶다고 할 때, gradient descent는 다음과 같은 식에 따라서 값을 계속 감소시켜나간다. (아래 식에서 $\gamma$를 learning rate 혹은 step size라고 부른다.)
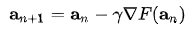
위 식을 해석하면, 기존의 점 $a_n$으로부터 이 점의 함수의 gradient(간단히 설명하면 미분값) 방향으로 점을 이동한 것을 다음 점으로 정의한다.

위 정의를 예시와 함께 해석해보자. 예를 들어, 아래 그림과 같이 생긴 함수가 있다고 하자. 이 함수는 $x=0$에서 최솟값을 가질 것이다. 만약 현재 점이 $x=0$보다 크다면 우리는 왼쪽 방향으로 이동해야 최솟값을 찾을 수 있을 것이고, 반대로 $x=0$보다 작다면 오른쪽 방향으로 이동해야 최솟값을 찾을 수 있을 것이다. 위에서 설명한 방향대로 이동을 하기 위해서는 우리는 x가 0보다 클 때는 음수로, x가 0보다 작을 때는 양수로 이동을 해야 한다. 이 방향을 다시 말하면, 최솟값을 찾기 위해서는 각 점에서의 기울기(gradient)의 음수 방향으로 이동을 해야할 것이다.

Learning rate
Learning rate는 우리가 원하는 방향으로 함수가 얼마나 크게 이동하면 좋을지를 결정하는 상수이다. 너무 큰 learning rate를 가지면 함수가 우리가 원하는 방향으로 minimize되지 않을 수 있고, 너무 작은 learning rate를 가지면 함수가 너무 느리게 minimize될 수 있기 때문에, 적절한 크기의 learning rate 선택은 아주 중요하다. 예를 들어, 우리가 다음과 같은 함수를 minimize하고 싶다고 하자.

이 함수의 global minimum은 (1,1)이고, 우리의 시작점은 (0,0)이다. 이를 각각 다른 learning rate 0.1, 0.6을 적용시켰을 때 어떻게 값이 수렴하는지에 대해 아래 그림을 통해 알아보자.

왼쪽 그림에서처럼 작은 learning rate를 가지면, 20번의 step을 지났음에도 불구하고 우리가 목표로 하는 minimum (빨간점)에 도달하지 못했음을 알 수 있다. 반면에 오른쪽 그림에서처럼 큰 learning rate를 가지면, 20번의 step이 지났을 때 값이 우리가 원하는 minimum 방향으로 수렴하지 않고 엄청 크게 튀는 것을 볼 수 있다. 그렇기 때문에 우리는 적절한 크기의 learning rate를 선택해야 한다. 이렇게 적절한 learning rate를 찾는 방법으로는 line search 등이 있는데 이에 대해서는 다음 포스팅에서 다루도록 하겠다.
한계
Gradient descent 방법은 가장 기본이 되고 널리 쓰이는 optimization 방법이지만 한계점을 가진다. 가장 큰 문제는 global minimum이 아닌 local minimum에 빠질 수 있다는 점이다.

Gradient descent 방법은 어떤 임의의 시작점으로부터 learning rate에 따라 반복적으로 이동하면서 optimal을 찾기 때문에, 위 그림에서 첫 번째 local optimum에서 optimization을 시작했다면, global optimum까지 도달하지 못하고 첫 번째 점에서 optimizaiton이 끝날 수 있는 것이다.
이번 글에서는 가장 기본적인 optimization 방법인 gradient descent가 무엇인지에 대해 알아보았다. 앞으로의 글들에서는 line search, newton's method 등 다양한 optimizaiton 방법들에 대해서도 알아보겠다.
References
1. Machine Learning: A Probabilistic Perspective (Adaptive Computation and Machine Learning Series) by Kevin P. Murphy (Author).
2. https://en.wikipedia.org/wiki/Gradient_descent
3. https://www.ibm.com/cloud/learn/gradient-descent
4. https://www.allaboutlean.com/polca-pros-and-cons/local-global-optimum/








최근댓글