Energy-based model은 데이터의 확률 분포를 energy function을 활용해 정의한 모델로, observed (혹은 more likely) data point에는 더 적은 에너지를, outlier (혹은 unlikely) data point에는 더 높은 에너지를 할당한다. 이러한 energy-based model은 현실 세계에서 더 안정적인 분자 구조가 더 적은 에너지를 가지는 현상 등과 일맥상통하기 때문에, 다양한 도메인의 생성 모델로 활용되고는 한다. 이번 글에서는 이 energy-based model (EBM)이 무엇인지에 대해 알아보겠다.
Motivation
많은 사람들이 흔히 알고 있는 생성 모델인 autoregressive model, VAE, normalizing flow 등의 모델들은 굉장히 제한적인 모델 구조를 가진다. 예를 들어, autoregressive model은 현재 time step 이전까지의 데이터에 대한 조건부 확률의 곱으로 현재 데이터 확률을 나타낸다는 제한을 가진다.
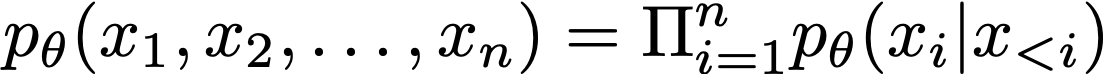
이러한 제한적인 모델 구조 문제를 해결하기 위해 GAN이라는 생성 모델이 등장하였다. GAN은 구분자와 생성자만 가지고 있으면, 이들이 어떤 형태이든 아무런 제약 없이 데이터를 생성할 수 있다. 하지만 GAN은 데이터의 likelihood를 정확히 계산할 수 없다는 한계점을 가진다. 하지만 energy-based model은, 제한적인 모델 구조를 가지지 않으면서 likelihood를 정확히 계산할 수 있는, 두 장점을 모두 취할 수 있는 생성 모델이다.
Energy-based model
데이터의 확률 분포는 항상 양수이고, 합했을 때에 1이 되어야 한다는 기본적인 성질을 가진다. 이를 만족시키기 위해 Energy-based model (EBM)은 확률 분포를 다음과 같이 parameterize하여 정의한다.

위 식에서 $Z(\theta)$는 normalizing constant로, p의 합이 1이 되도록 만들어주는 역할을 한다. 위와 같이 확률 분포를 정의했을 때의 이점은 두 가지가 있다. 첫 번째로, exponential을 활용함으로써 계산이 좀 더 용이해진다. 정규 분포, 감마 분포, 지수 분포 등 많은 확률 분포들은 exponential family 안에 속해 있는 경우가 많은데, 이들을 활용해서 계산하기가 좀 더 편하다는 장점이 있다. 두 번째로, 이러한 형태는 물리나 화학 등 자연에서 흔히 정의되는 확률 분포 형태이다. 예를 들어서, 어떤 시스템이 어떤 state에 속할 확률을 표현하는 Boltzmann 분포는 다음과 같은 형태를 가진다.

그렇기 때문에 위와 같은 형태로 확률 분포를 표현하는 것은 합리적인 선택이라고 할 수 있다. 또한 이렇게 표현함으로써 우리는 어떤 $f_\theta$도 자유롭게 사용할 수 있게 되고, 이에 따라 제한적인 모델 구조를 가지지 않는다는 장점 또한 가진다.
하지만 EBM도 치명적인 단점을 가지고 있는데, 이는 normalizing constant $Z$를 계산하는 것이 어렵다는 점이다. $Z$를 계산하기 위해서는 모든 데이터 포인트들에 대해 적분을 취해야 하는데, 이는 계산이 굉장히 복잡하기 때문에 현실적으로 불가능한 일이다. 그래서 우리는 이를 최대한 피하는 방법을 통해서 EBM의 학습과 샘플링을 진행한다.
Training
EBM 학습의 목적은 observed (혹은 more likely) data point에는 더 적은 에너지를, outlier (혹은 unlikely) data point에는 더 높은 에너지를 할당하여 각각이 더 높은 확률과 낮은 확률을 가지도록 만드는 것이다. 즉, 다음과 같은 그림을 목적으로 한다.

이를 달리 쓰면 결국, 우리는 다음과 같이 (observed) training data에 대해서 energy를 minimize하고 싶은 것이다. 이를 식으로 표현하면 다음과 같다.

하지만 우리는 $Z$를 직접적으로 구할 수는 없기 때문에, 이를 우회하는 방법을 사용해야 한다. 그 방법이 바로 contrastive divergence이다. Contrastive divergence는 Monte Carlo estimation 방법의 하나로, training data로부터 얻은 $f_\theta(x)$의 값과 현재의 distribution $p_\theta=\exp(f_\theta(x))/Z(\theta)$로부터 얻은 샘플의 $f_\theta(x)$의 값의 차이가 가장 큰 방향으로 gradient를 취해서 파라미터 $\theta$를 학습하는 방법이다. 이것이 결국 위 식을 maximize하는 것과 같은 이유는 다음과 같이 증명할 수 있다.

Sampling
다음으로, EBM의 샘플링을 가장 naive한 방법으로 생각해보면 각 샘플이 나올 확률을 계산하는 것은 $Z$의 계산 때문에 어렵지만, 두 개의 샘플 중 무엇이 더 확률이 클지를 비교하는 것은 쉽다.

그렇기 때문에 우리는 Monte Carlo 방법의 일종을 고려하여 두 개의 샘플을 뽑고, 둘 중에 더 확률이 높은 샘플을 그대로 두는 전략으로 샘플링을 진행할 수 있다. 즉, 이는 다음과 같은 과정을 통해 진행된다.
- 첫 번째 데이터 포인트 $x_0$를 정의한다.
- $x_t$에 어떤 노이즈를 더하여 $x'=x_t+$noise를 정의한다.
- 만약 $f_\theta(x')>f_\theta(x_t)$라면 $x_{t+1}=x'$으로 놓는다.
- 만약 $f_\theta(x')<f_\theta(x_t)$라면 $\exp(f_\theta(x)-f_\theta(x'))$의 확률로 $x_{t+1}=x'$로 놓는다.
- 2-4를 반복한다.
하지만 위의 간단한 방법은 converge하기 위해서 시간이 너무 오래 걸린다는 문제점을 가진다. 이를 해결하기 위해서 우리는 $Z(\theta)$의 계산이 필요 없는 score function을 활용한 Langevin dynamics를 통한 샘플링으로 이를 해결할 수 있다. 간단하게만 복습하면, score function은 log-lieklihood의 gradient를 뜻하고, Lagevin dynamics는 이러한 score function을 기반으로 하는 SDE를 활용하는 샘플링 방법을 의미한다. Score function은 데이터 $x$에 대한 gradient이기 때문에, $Z(\theta)$는 생략하여 계산을 할 수 있게 된다.

이는 다음과 같은 과정을 거친다.
- 샘플링이 쉬운 prior distribution $\pi(x)$로부터 첫 번째 데이터 포인트 $x_0$를 샘플링한다.
- Langevin dynamics 식을 따라 아래 식을 반복한다.

이번 글에서는 Energy-based model이 무엇인지에 대해 알아보았다. 아직 다루지 못한 normalizing flow, generative flow network 등 많은 생성 모델들이 있는데 차차 다루어보겠다.
References
Stefano Ermon. CS236: Deep generative models. Stanford. https://deepgenerativemodels.github.io








최근댓글