Normalizing flow는 invertible transformation을 활용하여 어떤 쉬운 분포로부터 실제 데이터 분포 사이의 transformation을 학습하는 생성 모델이다. Diffusion model로부터 시작되었고 flow matching까지 이어지는 생성 모델의 흐름은 정규 분포처럼 샘플링이 쉬운 데이터 분포로부터 어떤 하나의 값을 샘플링하여 이로부터 실제 데이터가 이루고 있는 복잡한 분포의 샘플을 얻어낸다는 프레임워크를 따른다. Normalizing flow의 개념을 이해하는 것이 flow matching을 이해하는 것과 직접적으로 관련이 있지는 않지만, 어떤 두 분포 사이의 transformation을 학습한다는 프레임워크를 공유하기 때문에, flow matching에 대한 글을 쓰기에 앞서 normalzing flow를 설명한다.
Overview
Normalizing flow는 정규 분포와 같은 쉬운 pror 분포 $p_0(z_0)$로부터 우리가 원하는 데이터가 배치되어 있는 target 분포 $p_K(z_K=x)$로의 transformation을 invertible한 매핑 f로 표현하는 생성 모델을 말한다.

이러한 과정을 통해 쉬운 prior 분포로부터 뽑은 noise를 우리가 원하는 데이터로 매핑할 수 있게 되고, 이러한 과정이 생성 모델의 역할을 하는 것이다.
Change of variables
Normalizing flow를 이해하기 위해서는 change of variables와 Detemeniant에 대한 이해가 필수적이다. 이를 최대한 쉽게 설명해보겠다. 우리가 어떤 평균이 0이고 분산이 1인 표준 정규 분포를 따르는 random variable X (아래 그림에서 파란색 선)를 가지고 있다고 하자. 그렇다면 Y=f(X)=1/3X 라는 random variable의 분포는 어떻게 표현할 수 있을까? 우리가 모든 X 값에 대해서 3을 나누기 때문에, 그 값의 분포는 아래 그림의 초록색과 같이 쪼그라들 것이다. 하지만 이렇게 값이 쪼그라들게 되면 적분했을 때 값이 1이 되어야 한다는 확률 분포의 성질(conserving probability mass)을 만족하지 못한다.

그맇기 때문에 우리는 확률 분포의 성질을 만족할 수 있도록 다시 전체 값에 3을 곱하여 빨간 선과 같이 Y의 확률 분포를 만들어준다. 이 때 3을 f inverse function의 x에 대한 determinant라고 부른다. 이를 식으로 표현하면 다음과 같다.
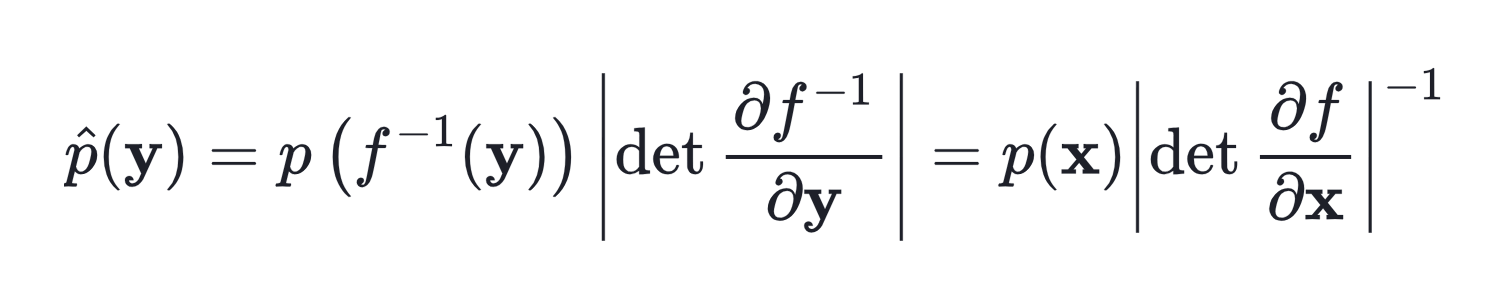
즉, 한 마디로 정리하면 어떤 두 분포 사이의 transformation이 필요할 때, 두 분포의 크기 차이를 맞춰주기 위해서 inverse function의 determinant를 곱해준다는 것이다. 이 determinant는 확률 분포의 volume이 줄어들거나 늘어나는 것을 조절하는 역할을 하고, change of variables는 이렇게 x의 density를 y로 바꾸는 등의 행동을 의미한다. 위와 같이 식이 정의되기 때문에, f는 1) 항상 역함수를 구할 수 있는 invertible한 함수여야 하고, 2) determinant를 구하기 쉬워야 한다. 이는 우리가 앞서 말한 문제 세팅인 간단한 prior 분포로부터 우리가 원하는 target 분포로 transformation을 할 때에도 그대로 적용된다.
Training of normalizing flow
그럼 결국 normalzing flow의 목표는 분포 사이의 transformation을 잘 해주는 적절한 $f_\theta$를 찾는 것이다. 이 때, 이 f는 1) 항상 역함수를 구할 수 있는 invertible한 함수이고, 2) determinant를 구하기 쉬운 형태로 정의된다. 이 적절한 f를 찾기 위해서는 적절한 objective를 가지고 학습을 진행해야 한다. 이 때 적절한 objective로는 다른 ML 알고리즘들처럼 data point x의 negative log-likelihood를 최소화하는 것이 사용된다. 이를 식으로 표현하면 다음과 같다.

Normalizing flow의 학습 objective
위 식에서 y는 데이터 포인트, x는 샘플링한 노이즈를 의미한다. 이 식은 위에서 설명한 change-of-variable 식에서 y를 데이터 포인트, x를 샘플링한 노이즈라고 생각하고 대입하면 도출된다. 이를 minimize하는 $f_\theta$를 찾음으로써 p는 점점 실제 데이터의 분포와 비슷하게 학습되고, 결국 prior 분포에 $f_\theta$를 적용함으로써 실제 데이터를 샘플링할 수 있게 되는 것이다.
Pros & cons
Pros
NF의 가장 큰 장점은 lieklihood를 완전히 정확하게 구할 수 있다는 점이다. VAE와 같이 어떤 variational bound를 활용해 학습하는 것이 아닌 정확한 MLE 식을 통해 학습되기 때문에 density를 정확하게 계산할 수 있다는 이점이 있다. 또한 noise로부터 data 혹은 data로부터 noise의 관계가 식을 통해 완전히 정확하게 매핑되고, sampling을 할 때에도 이 식을 계산만 하면 되기 때문에 샘플링 속도가 굉장히 빠르다는 이점이 있다.
Cons
NF의 단점은 f의 형태가 자유롭지 못하고, 역함수가 정의될 수 있고 determinant를 구하기 쉬운 형태로 제한된다는 것이다. 이러한 f에 대한 제한은 데이터가 완전히 유연하게 만들어지도록 하지는 못하기 때문에 샘플링을 할 때에 제약이 있을 수 있다. 또한 determinant의 계산 자체가 아무리 쉽게 만든다고 해도 높은 차원으로 갈수록 굉장히 시간이 오래 걸리고 복잡하다는 문제도 있다.
이번 글에서는 normalzing flow가 무엇인지에 대해 알아보았다. 다음 글에서는 이를 continous time transformation으로 확장한 continous normalinzg flow에 대해 알아보겠다.








최근댓글