Diffusion model은 데이터를 만들어내는 deep generative model 중 하나로, data로부터 noise를 조금씩 더해가면서 data를 완전한 noise로 만드는 forward process(diffusion process)와 이와 반대로 noise로부터 조금씩 복원해가면서 data를 만들어내는 reverse process를 활용한다. Diffusion model은 현재 image 쪽에서는 가장 잘 작동하는 generative model 중 하나이기 때문에 기본으로 알아놓으면 아주 유용할 것 같다. 그러므로 이번 글에서는 diffusion model이 무엇인지에 대해 알아보겠다.
Overview
Diffusion model은 위에서도 언급한 것처럼, data에 noise를 조금씩 더해가거나 noise로부터 조금씩 복원해가는 과정을 통해 data를 generate하는 모델이다. 이를 한 눈에 표현하면 아래 그림과 같다. 아래 그림에서 $x_0$는 실제 데이터, $x_T$는 최종 noise, 그리고 그 사이의 $x_t$는 데이터에 noise가 더해진 상태의 latent variable을 의미한다.
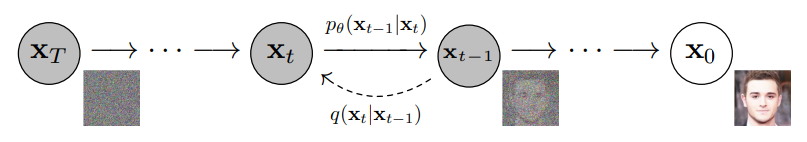
우선, 위 그림의 오른쪽에서 왼쪽 방향으로 noise를 점점 더해가는 forward process $q$를 진행한다. 그리고 이 forward process를 반대로 추정하는 reverse process $p$를 학습함으로써 noise($x_T$)로부터 data($x_0$)를 복원하는 과정을 학습한다. 그리고 이 reverse process를 활용해서 random noise로부터 우리가 원하는 image, text, graph 등을 generate할 수 있는 모델을 만들어내는 것이다. 그리고 이를 통해 결국, 우리는 실제 data의 분포인 $p(x_0)$를 찾아내는 것을 목적으로 한다. 그럼 이를 좀 더 자세히 살펴보겠다.
Reverse process
Reverse process $p$는 noise($x_T$)로부터 data($x_0$)를 복원하는 과정이다. 이는 최종적으로 random noise로부터 data를 generate하는 generative model로 사용되기 때문에 diffusion model을 사용하기 위해서는 모델링하는 것이 필수적이지만, 이를 실제로 알아내는 것은 쉽지 않다. 그러므로 우리는 $p_\theta$를 활용해서 이를 approximate한다. 이 때, 이 approximation은 Gaussian transition을 활용한 Markov chain의 형태를 가진다. 이를 식으로 표현하면 다음과 같다.
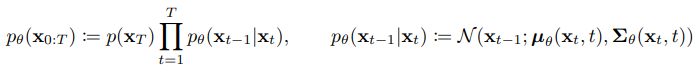
위 식에서, 각 단계의 정규 분포의 평균 $\mu_\theta$와 표준편차 $\Sigma_\theta$는 학습되어야 하는 parameter들이다. 그리고 위 식의 시작지점인 noise의 분포는 다음과 같이 가장 간단한 형태의 표준정규분포로 정의한다.

Forward process
Forward process $q$는 data($x_0$)으로부터 noise를 더해가면서 최종 noise ($x_T$)형태로 가는 과정이다. 우리가 이 과정의 분포를 알아내야 하는 이유는, reverse process의 학습을 forward process의 정보를 활용해서 하기 때문이다. Forward process는 reverse process와 비슷하지만 약간 다르게, data에 Gaussian noise를 조금씩 더하는 Markov chain의 형태를 가진다. 이를 식으로 표현하면 다음과 같다.

이제부터 약간의 수식 파티를 할 예정인데, 그냥 diffusion model이 이런거구나~ 하고 넘어가실 분들은 아래 내용은 읽지 않아도 좋지만 읽으면 더 좋다. 위와 같은 형태로 forward process를 표현할 때의 장점은 data가 주어졌을 때 임의의 timestep t 시점에서의 $x_t$를 자유롭게 sampling할 수 있다는 점이다. 어떤 data $x_0$가 주어졌을 때 $x_t$의 분포는 다음과 같다.

위 식에서 $\alpha$는 다음과 같은 식을 따른다.
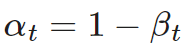

이의 증명은 다음과 같다. (증명은 생략해도 좋다.)
Training



- $L_T$: p가 generate하는 noise $x_T$와 q가 $x_0$라는 데이터가 주어졌을 때 generate하는 noise $x_T$ 간의 분포 차이
- $L_{t-1}$: p와 q의 reverse / forward process의 분포 차이. 이들을 최대한 비슷한 방향으로 학습한다.
- $L_0$: latent $x_1$으로부터 data $x_0$를 추정하는 likelihood. 이를 maximize하는 방향으로 학습한다.
이에 대한 증명은 다음과 같다.

결론적으로, 우리가 diffusion model을 학습할 때의 training loss는 정규 분포 사이의 KL divergence 형태로 쉽게 계산될 수 있는 것이다.
이번 글에서 우리는 VAE, GAN에 이어 다른 generative model인 diffusion model이 무엇인지에 대한 간단한 설명부터 어떻게 diffusion model이 정의되고 학습되는지에 대해서 수식을 통해 알아보았다. 이러한 diffusion model에도 DDPM, D3PM, NCSN 등 다양한 변형 형태가 있는데, 이들에 대해서도 찬찬히 살펴보도록 하겠다. 행복 대학원 중이지만 살짝 바빠서 블로그 쓰기가 쉽지 않은데 학기말 되면 더 쉽지 않을 것이므로 10월 연휴 때 열심히 쓰겠다.. 라고 매번 다짐..
References
1. Ho, J., Jain, A., & Abbeel, P. (2020). Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems, 33, 6840-6851.
2. https://lilianweng.github.io/posts/2021-07-11-diffusion-models/ -> 이 글은 정말 추천!








최근댓글