첫 머신러닝 글 ㅎㅎ 프로세스 마이닝만 하다가 알고 있던 것 다 잊어버릴 것 같아서 데이터 마이닝 글도 써야지 하고 계속 생각하고 있었는데, 머신러닝 수업 듣는 김에 정리하려고 한다.
사람들은 살아가면서 많은 결정을 하게 된다. 내일은 어떤 데이트를 해야 할지, 친구에게 어떤 선물을 줘야할지, 시험공부는 언제부터 시작해야 할지 등등. 예를 들어, 내일 애인을 만나기로 했다고 하자. 무작정 영화를 보고 밥을 먹는 것보다는, 저번 주에도 밖에서 데이트를 해서 이번 주에도 밖에서 만나면 힘들지 않을지, 내일의 날씨는 어떤지, 이번 주에는 혼자 있을 시간이 필요하지는 않은지 등의 많은 정보를 고려해서 결정하는 것이 평화로운 연애의 지름길일 것이다. 이렇게 우리는 의사 결정을 할 때에 많은 사전 정보들을 이용한다. 베이즈 결정 이론(Bayes Decision Theory)란, 기존에 가지고 있던 사전 정보를 활용하여 의사 결정을 할 때에 사용되는 이론이다.
Prior, Conditional Probabilities, Posterior Probabilities
우선, Bayes Decision Theory에서 사용되는 기본적인 확률 개념들부터 알아보겠다.
Prior
Prior이란, 우리가 데이터를 보기 전에, 사전 정보 없이 알 수 있는 확률 정보를 말한다. 예를 들어, a가 회를 먹고 싶어하는 확률, b가 고기를 먹고 싶어하는 확률이라고 하자. 여태까지 회를 12번 먹고 싶어 했고, 고기를 4번 먹고 싶어 했다. 그러면 a일 확률은 0.75, b일 확률은 0.25일 것이다. 이렇게 단순히 데이터를 보기 전에 알 수 있는 확률을 Priors(prori probabilities)라고 한다.
Conditional Probabilities
Conditional Probabilities는 우리말로 조건부 확률이다. 즉, Ck일 때에 x의 likelihood를 나타낸다.

예를 들어, x가 아래 그림에서 까만 픽셀의 수라고 하자.

a를 어떻게 쓰느냐에 따라 까만 픽셀의 수가 15가 될 수도, 25가 될 수도 있을 것이다. 이렇게 a라는 것이 주어진 상태에서 변하는 x 값의 분포를 나타내는 것이 conditional probability이다.
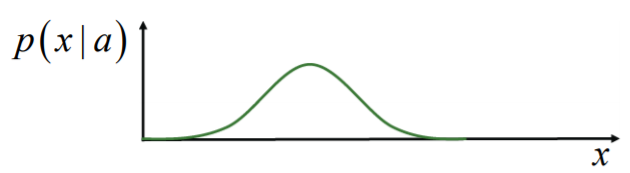
만약 a와 b의 조건부 확률을 다음과 같은 그래프로 함께 나타낼 수 있다고 하자.

위 그림과 같이 x 값이 15일 때, 글자가 a라고 판단하는 것이 좋을까 b라고 판단하는 것이 좋을까? p(x|a)가 p(x|b)보다 높기 때문에 a라고 판단하는 것이 좋을 것이다. 그렇다면 다음과 같이 x=25일 때는 a라고 판단하는 것이 좋을까 b라고 판단하는 것이 좋을까?
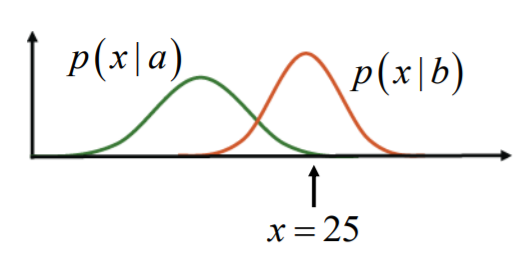
b라고 판단하는 것이 좋을 것이다. 그렇다면 다음과 같이 x=20일 때는 어떻게 판단하는 것이 좋을까?

애매하다. 하지만 만약 a의 prior이 0.75이고, b의 prior이 0.25라면? 그렇다면 그냥 찍어도 a일 확률이 더 높기 때문에 a를 선택하는 것이 맞을 확률이 더 높을 것이다. 이 prior까지 확률에 반영하려면 어떤 형태를 가져야할까? 다음과 같이 likelihood에 prior를 곱한 형태를 가지면 될 것이다.
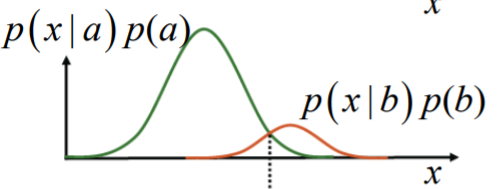
Posterior Probabilities
Posterior probability는 주어진 input(x)에서 a 클래스가 될 확률 혹은 b 클래스가 될 확률을 말한다. 즉, 어떠한 사전 정보가 주어졌을 때 어떤 결정을 해야하는지를 알려주는 확률이다. 그것은 베이즈 정리에 따라 다음과 같은 식으로 표현할 수 있다.
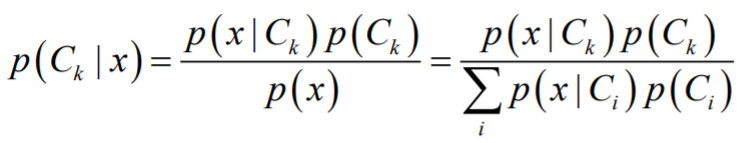
여기에서 가운데 부분의 분자 부분이 위에서 말한 likelihood * prior의 형태를 가짐을 알 수 있다. 그래서 우리는 posterior probability를 다음과 같이 쓸 수도 있다.
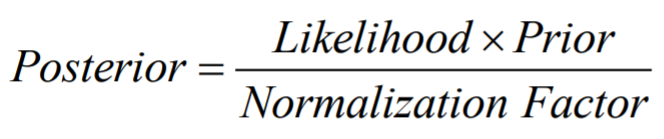
Decision Making
위에서와 같이 각 결정에 대한 확률 분포를 구했으면, 이제 결정을 할 차례이다. 결정을 할 때에는 어떤 기준으로 해야할까? 그 기준에는 여러 가지가 있을 수 있다.
Minimize the probability of misclassification
대부분의 의사결정은 잘못 판단할(misclassification) 확률을 낮추는 것을 목적으로 할 것이다. 그렇다면 이 잘못 판단할 확률을 어떻게 계산할 수 있을까? 만약 우리가 x가 x hat(눈웃음 모자 쓴 x)보다 작으면 C1이고, 그 이상이면 C2라고 판단하기로 했다고 하자.

그렇다면 위 그림에서 R1이 우리가 C1으로 판단하기로 한 부분이고, R2가 C2로 판단하기로 한 부분일 것이다. 그렇다면 우리가 여기서 잘못판단할 확률은 R1에 속했는데(C1으로 판단하기로 했는데) 실제로는 C2일 확률(그림 상 초록색 + 빨간색)과 R2에 속했는데 실제로는 C1일 확률(그림 상 파란색)을 더한 것일 것이다. 이를 수식으로 표현하면 다음과 같다.

이를 최소화하는 것이 decision making의 한 목적이 될 수 있다.
Minimizing the Expected Loss
Misclassification만을 최소화하면 최고의 의사결정이 될 수 있을까? 회를 엄청 좋아하는 사람이 있다고 하자. 이 사람이 고기가 먹고 싶었는데 회를 먹였을 때의 분노와 회가 먹고 싶었는데 고기를 먹였을 때의 분노가 같을까? 물론 다를 것이다. 이렇게 같은 msiclassification이라도 그 손해가 달라질 수 있기 때문에 우리는 이에 대해서도 고려를 해야 한다. 이를 expected loss를 최소화하는 방향으로 의사결정을 한다고 한다. 이는 다음과 같은 식으로 표현할 수 있다.

즉, posterior probability에 loss function을 곱한 값의 합이 최소가 되는 방향으로 의사결정을 하면 expected loss가 최소화되는 방향으로 의사결정을 할 수 있는 것이다.
Reject Option
모든 결정을 expected loss나 misclassification을 최소화하는 것처럼 확률 기반으로 하지 않는 방법도 존재한다. 예를 들어, 다음과 같은 posterior probability 분포가 있다고 하자.

위 그림에서, 초록색 경계를 기준으로 첫 번째와 세 번째 부분에서는 각각 C1과 C2라고 비교적 확신을 가지고 판단할 수 있다. 하지만 그 가운데 부분에서는 두 확률이 그렇게 큰 차이가 나지 않기 때문에 그렇게 확신할 수가 없고, 실제로 misclassification의 대부분이 저 부분에서 일어날 것이다. 저 확신할 수 없는 부분을 우리는 reject region이라고 부른다. 저 reject region에서 우리는 확률에 기반하여 자동으로 의사결정을 하기보다는, 사람이 직접 다른 것을 판단하여 의사결정을 하는 등의 다른 방법을 사용하여 의사결정을 함으로써 오류를 줄일 수 있다.
이번 포스팅에서는 Bayes Decision Theory에 대해 알아보았다. 최대한 수식을 줄이고 쉽게 설명하도록 노력했는데 머신러닝은 산수를 배제할 수 없기 때문에 어쩔 수 없다 하하.. 미래의 내가 계속 성실하게 머신러닝 포스팅을 하기를 빈다 ㅎㅎ
References
1. Course: Machine Learning. Prof. B. Leibe. RWTH.








최근댓글