Association Rule의 적용을 위해서는, 각 item들이 각 itemset 안에서 어떤 빈도로 출현했는지, 어떤 item과 함께 나왔는지를 세는 것이 필수적이다. (Association Rule이 무엇인지 궁금하다면 다음 포스팅을 참고한다.)
2019/08/01 - [Data Mining - Thoery] - Association Rule (연관 규칙)이란?
Association Rule (연관 규칙)이란?
첫 데이터 마이닝 포스팅이다. 데이터 마이닝은 관련 포스팅이 너무 많기도 하고, 나보다 잘 아시고 글 잘 쓰시는 분들이 세상에 차고 넘칠 것 같아 (아 물론 프로세스 마이닝도 나보다 세상에 잘 아시는 분들이..
process-mining.tistory.com
하지만 데이터셋이 큰 경우, 이를 모든 후보 itemset들에 대해서 하나하나 검사하는 것은 굉장히 비효율적이다. 이러한 문제를 해결하기 위해 제시된 것이 FP-growth 알고리즘이다. 이번 포스팅에서는 이 FP-growth 알고리즘에 대해 알아보겠다.
Build FP-tree
FP-growth 알고리즘을 적용시키기 위해서 가장 먼저 해야 할 일은 FP-tree를 만드는 것이다. 이 FP-tree를 만듦으로써 우리는 기존에 데이터셋을 모두 찾아보면서 찾아야했던 frequent itemset들을 FP-tree 하나에서만 찾을 수 있게 된다. 이를 만드는 과정을 예시와 함께 알아보도록 하겠다. 우선, 우리에게 다음과 같은 데이터셋이 있다고 하자.

1. 모든 각각의 item들에 대해 전체 데이터셋에서 나온 빈도를 계산한다.
데이터셋의 모든 item들에 대해 빈도를 계산한다. 우리의 예시에서는 초장이 9+1=10으로 10번, 과메기가 40+50+1=91번, 김이 50+1=51번 나타났다. 이를 빈도가 높은 순서대로 표현하면 과메기:91, 김:51, 초장:10이다.
2. itemset 하나씩 tree에 더함으로써 tree를 만들어준다.
이제 tree를 만들 차례이다. 우선, 맨 처음에 0 node를 하나 만든다.

그리고 각 instance를 하나씩 더해주면서 tree를 만들어간다. 이 때, 빈도가 높은 item이 더 0에 가까운 node가 된다. 예를 들어, 우선 {과메기, 김} itemset으로 tree를 만든다고 하자. 그러면 다음과 같은 형태가 된다.
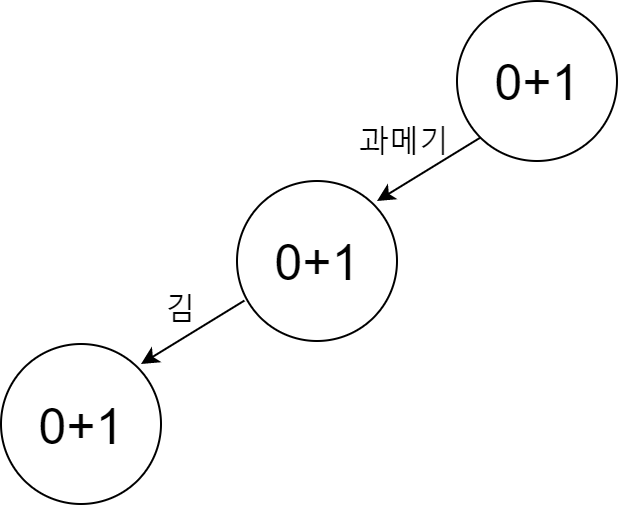
빈도가 더 높은 과메기가 더 가까운 곳에 위치하는 tree가 만들어졌다. 이 단계에서 우리가 {과메기, 김, 초장} itemset을 추가한다고 하자. 그러면 다음과 같은 형태가 될 것이다.

여기서 {초장} itemset을 추가한다고 하자. 그러면 다음과 같은 형태가 될 것이다.
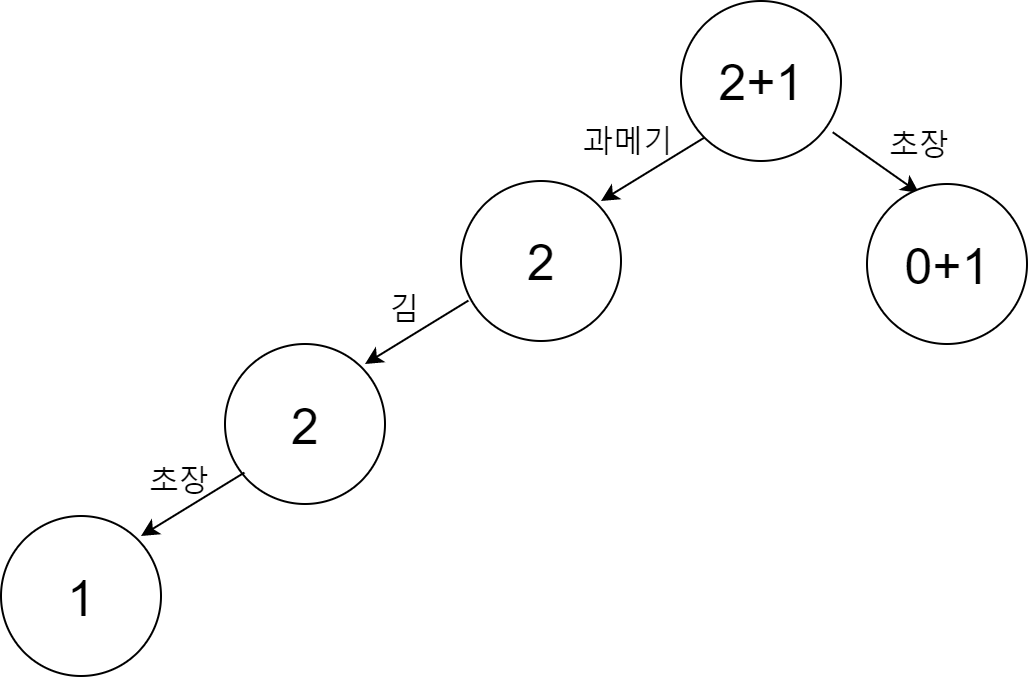
이런 식으로 dataset 안의 모든 itemset에 대해 tree를 만들 수 있다. 그러면 최종적으로 다음과 같은 FP-tree를 얻을 수 있다.
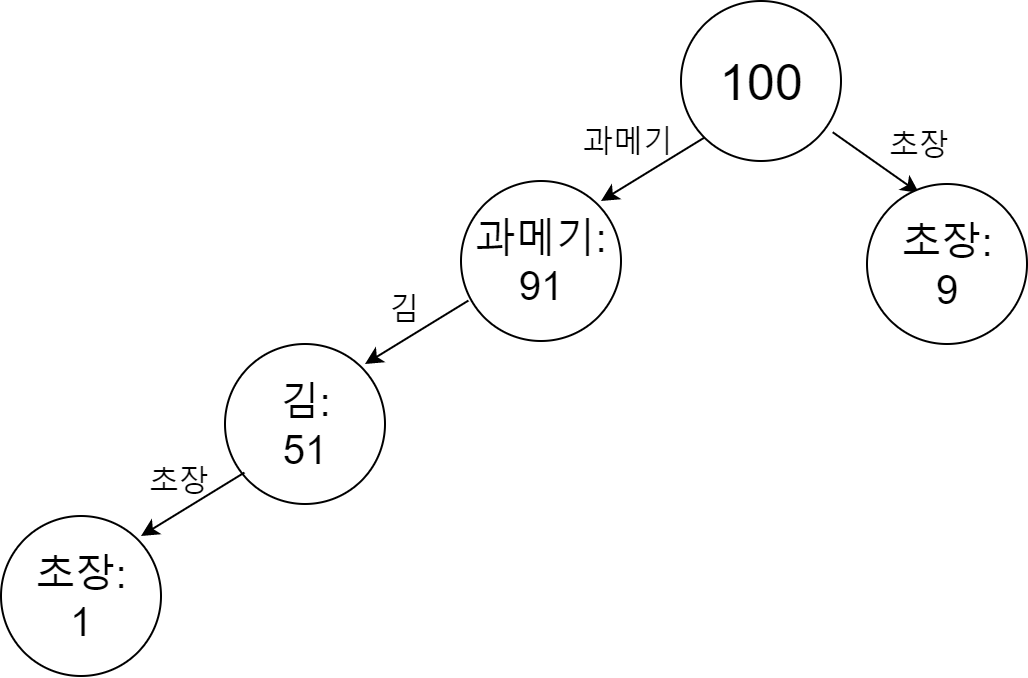
이렇게 dataset 안의 모든 itemset의 정보를 반영하는 FP-tree를 만들어낼 수 있다. 이 FP-tree를 이용하면 아주 쉽게 support 값을 구할 수 있다. 예를 들어, 우리의 tree에서 {김, 과메기}의 support를 구하고 싶다고 하자. 김은 무조건 과메기와 함께 나타나기 때문에 김의 frequency만 고려하면 되고, 이는 51이므로 {김, 과메기}의 support는 51이 된다. 이러한 방법으로 우리의 dataset의 support를 모두 구하면 다음과 같다.
| item sets | support |
| {과메기} | 91 |
| {김}, {김, 과메기} | 50 |
| {초장} | 10 |
| {과메기, 김, 초장} | 1 |
우리의 예시 데이터는 굉장히 간단한 데이터였기 때문에 한 눈에 각 itemset들의 support를 구할 수 있었다. 하지만 데이터의 크기가 크거나 복잡한 데이터는 이러한 방법으로 support를 구할 수는 없을 것이다. 그러므로 다음 단계에서는 복잡한 데이터에서 support를 쉽게 계산하는 방법에 대해 알아볼 것이다.
Mine FP-tree
다음과 같은 조금 더 복잡한 예시 데이터셋이 있다고 하자.
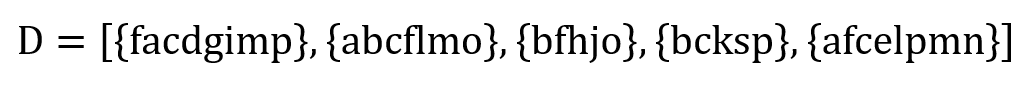
1. frequency를 이용해 infrequent item을 필터링한다.
우선, 각 item들의 frequency를 모두 계산해준다. 이는 다음과 같다.
| item | frequency |
| f, c | 4 |
| a, b, m ,p | 3 |
| l, o | 2 |
| d, e, g, i, j, h, k, n, s | 1 |
우리는 frequency가 3 이상인 아이템들만 고려한다고 가정한다. 즉, 우리가 원하는 minimum support가 3인 것이다. 그러면 우리는 다음 아이템들만을 고려할 것이다.
| item | frequency |
| f, c | 4 |
| a, b, m ,p | 3 |
제거된 infrequent item들을 제외하고 itemset을 다시 만들면 다음과 같다.
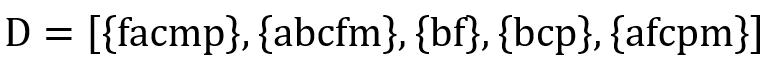
2. Filtered Dataset을 이용해 FP-tree를 만든다.
위에서 했던 과정과 같이 이번에는 새로운 데이터셋을 이용해 FP-tree를 만들어준다. (이 과정은 생략한다.) 그러면 다음과 같은 FP-tree가 도출된다.

3. frequent item들 각각을 postfix로 놓고 각 item별로 recursive하게 support를 구한다.
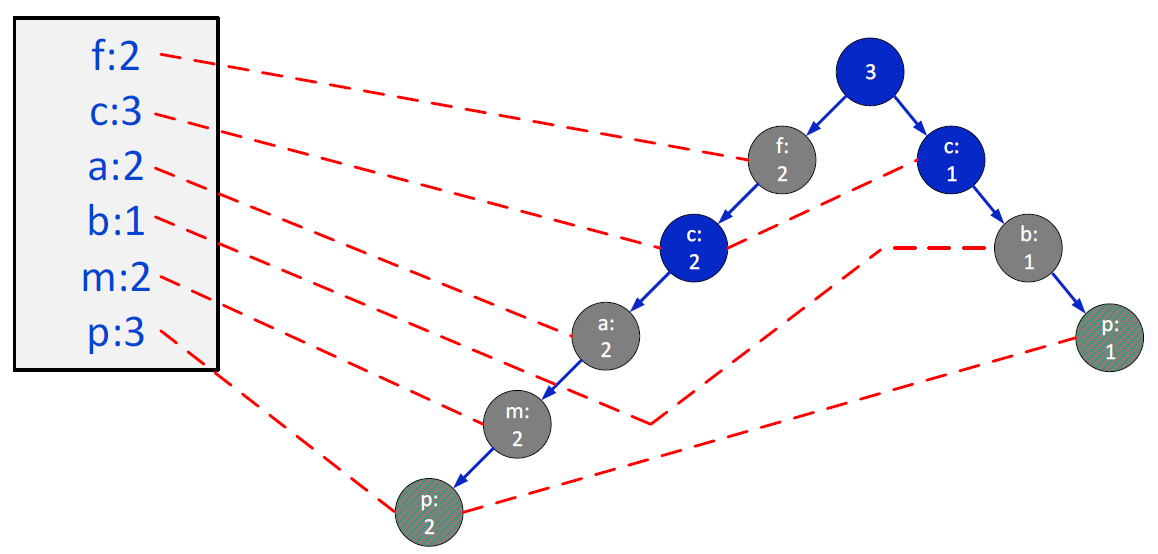
말이 복잡하다. 예시를 통해 설명하도록 하겠다. 우선, frequent item인 f, c, a, b, m, p 중 p를 먼저 살펴보자. 우선, 우리의 itemset에 {p}의 support가 3인 것을 넣을 수 있다. 다음으로, 우리의 FP-tree 중 p가 포함되는 tree 가지만을 남기고 다른 것은 고려하지 않는다. 그러면 tree는 다음과 같은 형태가 된다.

이에 따라서 다시 각 item의 빈도를 구하면 위 그림의 왼쪽 박스와 같다. 우리의 minimum support는 3이기 때문에 이를 만족하는 item은 아래 그림과 같이 p와 c밖에 없다.
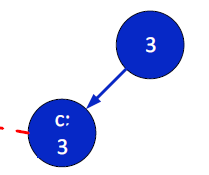
그러므로 우리는 최종적으로 다음과 같은 FP-tree를 얻게 되고, {p, c} itemset은 support가 3이 되므로 조건을 만족하는 itemset이다.
다음으로, m을 살펴보자. 우선, 위에서와 같이 우리의 itemset에 {m}의 support가 3인 것을 넣을 수 있다. 다음으로, 우리의 FP-tree 중 m이 포함되는 tree 가지만을 남기고 다른 것은 고려하지 않는다. 그러면 tree는 다음과 같은 형태가 된다.

이에 따라서 다시 각 item의 빈도를 구하면 위 그림의 왼쪽 박스와 같다. 우리의 minimum support는 3이기 때문에 이를 만족하는 item은 아래 그림과 같이 m, f와 c와 a가 된다.
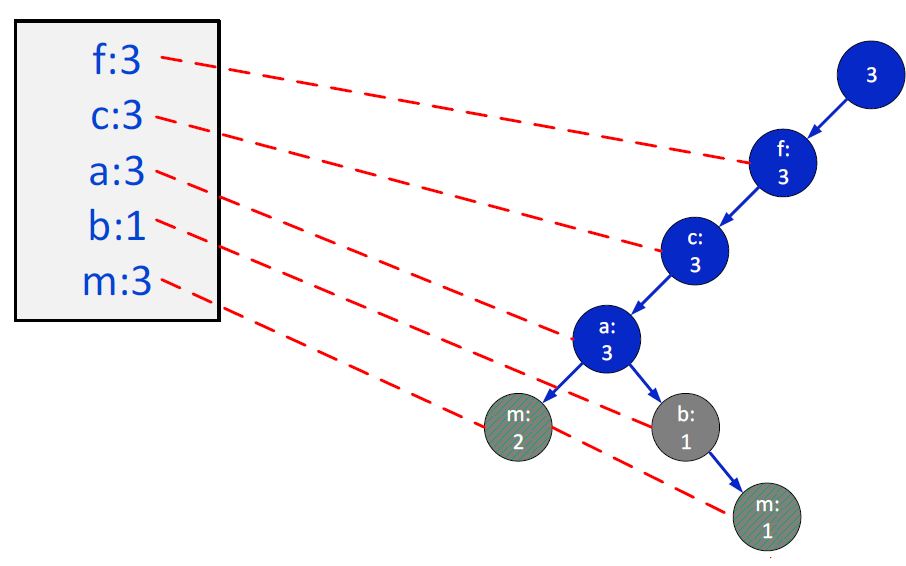
그러므로 우리는 최종적으로 위 그림에서 파란색의 FP-tree를 얻게 된다. 그러므로 우리는 recursion을 통해 {m, f}, {m, c}, {m, a}, {m, c, a}, {m, f, c}, {m, f, a}, {m, a, c, f} itemset의 support가 3이 됨을 알 수 있다.
모든 frequent item들에 대해 이와 같은 과정을 적용시킴으로써 support가 3 이상인 모든 itemset을 얻을 수 있다. (모든 과정은 생략한다.) 그 결과는 다음과 같다.
| item | frequency |
| {f}, {c} | 4 |
| {a}, {b}, {m}, {p}, {p, c}, {m, a, c, f}, {m,c, f}, {m, a, f}, {m, a, c}, {m, a}, {m, c}, {m, f}, {a, c, f}, {a, c}, {a, f}, {c, f} | 3 |
이러한 과정을 통해 모든 데이터셋에 대해 minimum support를 만족하는 itemset을 구할 수 있다.
이번 포스팅에서는 FP-tree와 함께 FP-growth 알고리즘이 무엇인지에 대해 알아보았다. FP-growth 알고리즘은 dataset 전체에 대한 순회를 FP-tree를 만들 때에만 하면 되기 때문에 매우 빠르고 메모리에 무리도 적다는 강력한 장점을 가진다. 이를 Association Rule, Sequence MIning에서 적절히 활용한다면 더 효율적인 처리가 가능할 것이다.








최근댓글