어떤 데이터의 분포를 파악하는 것은 데이터 분석에 있어서, 나아가 머신 러닝에 있어서 굉장히 중요한 단계이다. 하지만 실제 데이터는 대부분의 경우에 정규 분포와 같은 예쁜 분포 형태를 따르지 않고, 어떤 분포를 따르는지 전혀 알 수가 없다. 이런 경우에 데이터의 분포를 추정하여 확률 밀도(probability density)를 추정하는 방법에는 histogram, kernel density estimation, K-nearest neighbor 등 다양한 방법이 있다. 이번 포스팅에서는 그 중에서 kernel density estimation (kernel method), 그리고 그 대표적인 방법인 parzen window에 대해 알아볼 것이다.
Motivation
우리의 목표는 확률 밀도(probability density), 즉 p(x)를 구하는 것이다. 이는 일정한 단위 안에 우리의 데이터가 몇 개나 포함되는지의 값과 같다. 그러므로 우리는 p(x)가 다음과 같은 식에 비례함을 알 수 있다. 여기서 N은 전체 데이터 샘플의 수, K는 해당 region 안에 있는 데이터의 수, 그리고 V는 해당 region의 부피를 말한다.

이 식을 통해 우리는 일정 단위 안에 우리의 데이터가 포함될 확률, 즉 확률 밀도를 구할 수 있다. 이 식에서 N 값은 데이터 전체의 크기이기 때문에 고정이다. 이 때, region의 부피(크기)(V)를 고정하고 그 안에 몇 개가 들어갈 수 있는지(K)를 찾아냄으로써 확률 밀도를 구하는 방식을 kernel method라고 한다. (이와 반대로, 안에 들어갈 개수(K)를 고정하고 그 부피(V)를 결정하는 것을 K-nearest neighbor라고 한다. 이는 다음 포스팅에서 다룰 것이다.)
Parzen Window
이러한 kernel method 중 대표적인 방법이 parzen window이다. 다음과 같은 평면이 있다고 하자.

Kernel Method는 일정한 부피(혹은 넓이) 안에 들어갈 데이터의 개수를 세는 방식이다. 즉, 우리의 기준점을 (0,0)이라고 했을 때 위 그림에서 K는 네모 안의 점 개수인 5가 되고, 사각형의 길이를 h라고 하면 V는 h^2이 되는 것이다. 이를 식으로 나타내면 다음과 같다.

이러한 식을 데이터 포인트 u의 kernel function이라고 한다. 즉, 데이터 u가 h의 길이를 가지는 D dimension 안에 있으면 1, 아니면 0이 되는 함수인 것이다. 이 kernel function을 이용해 우리가 찾기를 원하는 값인 K와 V 값을 식으로 나타내면 다음과 같다.

위 식을 해석해 보면, K는 x를 중심으로 한 region 안에 포함된 데이터 x_n의 개수를 말하고, V는 이 region의 부피를 말한다. 이 식을 기반으로 하여 우리가 원하는 확률 밀도를 구해보면 다음과 같이 표현할 수 있다.

하지만 이러한 parzen window 방식은 각 큐브의 경계값 위에 데이터가 있을 때는 이를 처리하는 것이 모호하다 (discontinuity)는 단점을 가진다. 이의 해결을 위해 우리는 다른 kernel function을 이용할 수 있다.
Gaussian Kernel
우리의 kernel function으로 Gaussian Kernel을 이용한다고 하자. 그러면 kernel function은 다음과 같이 표현할 수 있을 것이다.
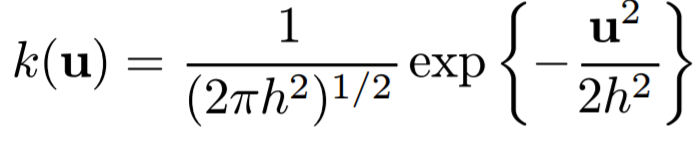
이 식을 기반으로 하여 K 값과 V 값을 계산하면 다음과 같다.

그리고 이 K와 V를 이용하여 probability density estimation을 하면 다음과 같은 식이 유도된다.
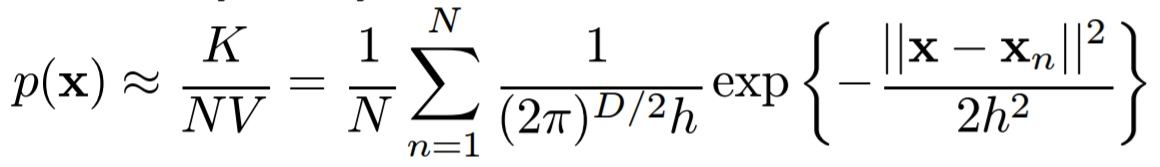
이러한 방식으로 다양한 kernel function을 이용하여 kernel method를 이용해 probability density estimation이 가능하다. 다음 포스팅에서는 K-nearest neighbor를 이용한 probability density estimation에 대해 알아보겠다.
References
1. Machine Learning. Prof. Bastian Leibe. RWTH. 2019.








최근댓글