Linear regression은 데이터 간의 선형적인 관계를 가정하여 어떤 독립 변수 x가 주어졌을 때 종속 변수 y를 예측하는 모델링 방법이다. 이번 글에서는 머신 러닝 공부를 시작하면 가장 먼저 배우는 개념 중 하나인, linear regression에 대해 알아보겠다. 이번 포스팅은 maximum likelihood에 대한 이해가 있다고 가정한다.
Motivation
다음과 같은 데이터가 있다고 하자. 우리는 x값을 넣었을 때 y값을 예측하는 모델을 만들고 싶다.

이를 예측하는 하나의 선을 정하는 과정에서, 우리는 다음과 같은 여러 선들을 그릴 수 있을 것이다.

두 선 중 어떤 것이 데이터(점)를 더 정확하게 예측하는 것처럼 보이는가? 모두가 왼쪽이 더 정확하게 예측한다고 생각할 것이다. 왜 그렇게 생각했을까? 아마 각 x 점 (1, 2, ..., 10)에서의 y 값과 파란 선이 각 x점에서 가리키는 y 값이 겹치는 부분이 많고, 차이도 적게 나기 때문일 것이다. 이렇게 쉽게 말하면, 가장 데이터를 정확하게 예측하는 식을 찾는 과정을 우리는 linear regression이라고 한다.
정의
* 수학이 싫은 분들은 넘어가도 좋습니다.
우리는 위에서, x 값을 넣었을 때 실제의 y에 가장 가까운 y 값을 예측하는 식을 찾는 과정을 linear regression이라고 불렀다. 이를 수학처럼 보이는 식으로 나타내면, 아래 식처럼 나타낼 수 있다.

즉, 우리가 linear regression을 할 때는 epsilon을 가장 작게 하는 w^T값을 찾아, w^Tx값이 y(x) 값과 가장 가까워지도록 만드는 것을 목표로 하는 것이다. 이 식에서 우리는 x를 input vector, w를 weight vector, epsilon을 residual error라고 부른다.
Linear Regression을 달리 표현하면, 다음과 같이 표현할 수 있다.
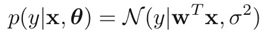
즉, x와 parameter(theta)가 주어졌을 때, y가 해당 분포를 따를 확률을 최대화하는 분포를 찾는 것을 linear regression이라고 할 수 있는 것이다. 그리고 여기서, y가 해당 분포를 따를 확률(posterior)를 정규분포(정확히는 likelihood를 정규분포, prior를 uniform distribution)라고 가정하는 것을 우리는 linear regression 중에서도 Least squares이라고 한다. 그렇다면 여기서, 우리는 x가 단 하나의 값일 때밖에 예측할 수 없는 것일까? 당연히 아니다. 위의 식을 좀 더 일반화시키면 다음과 같이 표현할 수 있다.

여기서 phi(x)는 다양한 non-linear function으로도 표현될 수 있다. 이렇게 모든 w 값들 중에서 x 값을 넣었을 때 가장 y 값을 잘 예측하는 w를 찾는 과정을 우리는 linear regression이라고 한다.
Maximum Likelihood
그렇다면 linear regression에서 maximum likelihood를 어떻게 적용할 수 있을까? Maximum likelihood를 이해하고 있다면 간단하다. 우리는 log likelihood를 다음과 같은 식으로 표현할 수 있다. (이에 대한 자세한 설명은 위 링크 포스팅으로 대체한다.)

이를 위에서 구했던 linear regression의 likelihood 식으로 바꿔주기만 하면 linear regression의 maximum likelihood를 구할 수 있다. 즉, 이 likelihood를 최대화하려면 상수들을 제외하고 RSS 값을 최소화해야하는 것이다.

위 식에서 RSS는 Residual Sum of Squares (혹은 SSE. Sum of Squared Errors)를 말하고, 그것은 다음 식처럼 표현할 수 있다.
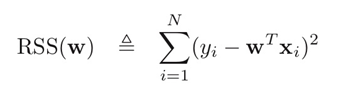
즉, RSS는 실제 값과 예측 값의 차이의 제곱의 합을 의미한다. 이는 다음과 같은 l2 norm 형태로도 표현될 수 있다.

즉, linear regression은 RSS값을 최소로 만드는 w 값을 찾는 과정인 것이다.
이번 포스팅에서는 머신러닝의 가장 기본적인 개념 중 하나인 linear regression에 대해 알아보았다.
예전에는 머신러닝 블로그 잘 쓰는 분들이 너무 많아서 쓰고 싶다는 생각이 잘 안 들었는데, 요즘 들어 기본이 중요하다는 생각이 계속 들어서 간만에 쓴 기본적인 머신러닝 글. 너무 쉬운걸 쓴 것 같기는 하다... 2020년에 글 100개 쓰려면 비둘기집 원리에 의해서 이틀 연속으로 글 쓰는 날이 무조건 존재해야 하기 때문에 (현실적으로 불가능.. 아니 사실 안 누워있으면 가능.. 하지만 안 누워있기가 불가능하니까 삼단논법에 의해 불가능..) 소소하게 2020년 갈 때까지 블로그 일주일에 2개 무조건 쓴다.. 제발....
References
Machine Learning: A Probabilistic Perspective (Adaptive Computation and Machine Learning series) Illustrated Edition. by. Kevin P. Murphy (Author) › Visit Amazon's Kevin P. Chapter 7.








최근댓글