Method of Moments 설명 (MOM이란?)

우리는 어떤 데이터에 대한 parameter를 추정하고 싶을 때, Maximum Liklihood Estimation 혹은 MAP Estimation 등의 방법을 주로 사용한다. 이외에도 Empirical Risk Minimization(ERM), Method of Moments(MOM) 등 parameter를 추정하는 다양한 방법들이 존재한다. 이번 포스팅에서는 그 중에서도 log likelihood의 미분이 힘들어 MLE를 계산하기가 어려운 상황일 때에 사용하는 방법인 Method of Moments에 대해서 알아보겠다. 

정의

 MOM은 이론적으로 계산한 moment 값인 theoretical moment와 실제 moment 값인 empirical moment의 차이가 최소화되는 방향으로 parameter를 계산한다. 이 때, moment의 차수인 k는 1부터 K까지의 정수이고, K는 parameter의 개수가 된다. 이론적 moment 값은 아래와 같이 정의할 수 있다.

이론적 moment

 그리고 실제 moment 값은 아래 식에 따라 계산할 수 있다.

실제 moment

그러므로 MOM은 모든 k에 대해 mu_k = mu_k hat의 식을 푸는 것을 목적으로 하는 것이다. 

예시

Univariate Gaussian

 정규분포에서는 parameter가 평균, 분산의 두 가지가 있으므로 K=2이다. 그러므로 정규분포에 대한 1차, 2차 theoretical moment와 empirical moment는 아래와 같이 표현할 수 있다. (mu_1 / mu_2가 theoretical moment, y_bar과 s^2이 empirical moment이다.)

정규분포의 1 / 2차 moment

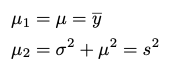
 그렇다면, 이 상황에서 parameter는 무엇으로 추정할 수 있을까? 우선, 1차 모멘트부터 살펴보자. 1차 모멘트가 이론적 모멘트와 같은 값이 되려면 mu는 전체 값들의 합을 데이터의 개수로 나눈 값, 즉 평균이 되어야함을 알 수 있다.

mean의 추정치

2차 모멘트가 이론적 모멘트와 같은 값이 되려면 sigma의 제곱이 아래 식과 같이 모든 값의 제곱의 합의 평균에서 평균의 제곱을 뺀 값이 되어야 한다. 

sigma의 추정치

이는 MLE에서 구했던 parameter estimation 결과와 같다. 

Uniform Distribution

 항상 MLE와 MOM의 결과가 같은 것은 아니다. 그 예시로는 uniform distribution이 있다. Y가 theta_1에서 theta_2 사이의 uniform distribution을 따른다고 할 때, 우리는 이의 pdf를 아래와 같이 정의할 수 있다.

uniform random variable Y의 pdf

 parameter과 theta_1과 theta_2의 두 개이므로, 이론적인 1차 moment와 2차 moment를 구해보면 아래와 같다. 

uniform 분포의 1 / 2차 theoretical moment

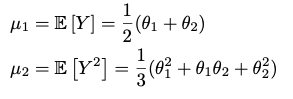
이를 활용하여 각 theta 값(parameter)을 구하면 아래와 같이 표현할 수 있다.

도출한 theta 값

 우리는 MOM의 적용을 위해 이 이론적 moment와 empirical moment를 같게 만들어야할 것이다. 예를 들어 [0,0,1,0,0]이라는 데이터가 있다고 하자. 그렇다면 이의 1 / 2차 empirical moment는 각각 1/5가 될 것이다. 이를 활용하여 parameter estimation을 진행하면, 우리는 -0.493이라는 theta_1 값과, 0.893이라는 theta_2 값을 도출할 수 있다. 하지만 theta_2가 0.893이기 때문에, 우리의 원 데이터에 있는 1이라는 값을 뽑아낼 수 없다. 즉, 이 parameter estimation이 틀린 것이다. 이와 같이 MOM은 틀린 parameter을 종종 도출하기도 한다.

활용

 MOM의 장점은 미분과 같은 계산이 필요하지 않기 때문에 계산이 복잡한 경우 없이, 쉽게 계산할 수 있다는 점이다. 하지만 위에서의 uniform distribution 예시에서 볼 수 있듯이, MLE와는 달리 항상 정확한 답을 도출해내지는 못한다. 그렇기 때문에 실제 활용에서는 MOM의 계산 효율성과 MLE의 정확성을 모두 취하기 위해 MOM의 값을 활용하여 MLE의 initialization을 진행하기도 한다.

 

 이번 포스팅에서는 또 다른 parameter estimation 방법인 Method of Moments에 대해 알아보았다. 상황에 따라 적절한 parameter estimation을 활용해 원하는 parameter를 추정할 수 있어야할 것이다.

References

1. Probabilistic Machine Learning: An Introduction by Kevin Patrick Murphy. MIT Press, February 2022.