우리는 그래프를 활용해서 어떤 예측을 할 때, 하나의 노드가 어떤 특성을 가지고 있는지를 예측하기도 하지만 (node classification), 두 노드 사이의 관계를 예측하기(link prediction)도 한다. 이번 글에서는 두 노드 사이의 관계를 표현하는 가장 기본이 되는 척도인 neighborhood overlap, 그 중에서도 local overlap measure에 대해서 알아보겠다.
우선, 두 노드 사이의 neighborhood overlap은 말 그대로 몇 개의 이웃(직접 연결된 노드)을 공유하고 있는지를 의미한다. 이를 식으로 나타내면 다음과 같다.

위 식은 다른 말로 common neighbors라고도 부른다. 예를 들어, 다음과 같은 그래프가 있다고 하자.

그림에도 나타나 있듯이, 노드 A의 neighborhood는 C이고, 노드 B의 neighborhood는 B이다. 그러므로 노드 A와 B의 common neighbors는 1이다.
local overlap measure
local overlap measure는 common neighbors와 같이 단순히 두 노드가 공유하는 이웃 노드들의 수를 활용한 다양한 measure들이다.
Sorenson index
Sorenson index는 다음과 같이 정의한다.

위 식에서 d는 각 노드의 node degree를 의미한다. 즉, 두 노드가 공유하는 노드의 개수를 각 노드에 연결된 이웃의 수로 normalize한 것이다. 이렇게 normalize를 하는 이유는, 단순히 common neighbors만 도출하게 되면 그냥 노드에 연결된 이웃이 많은 노드(node degree가 높은 노드)에 연결된 엣지들만 중요한 엣지로 여겨질 수 있기 때문이다. 위 예시 그래프에서 A와 B 사이의 Sorenson index를 구하면, A의 degree는 1, B의 degree는 2이므로 (2*1)/(1+2)=0.67이 된다.
Salton index
Salton index는 Sorenson index와 비슷한 형태를 가지고 있다.
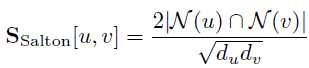
Salton index는 common neighbors를 두 노드의 degree 곱의 제곱근 값으로 normalize한다. 위 예시 그래프에서 A와 B 사이의 Salton index를 구하면 (2*1)/(root 2)= 1.41이 된다.
Jaccard overlap
Jaccard overlap은 다음과 같이 정의한다.
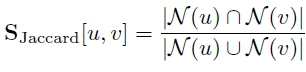
Jaccard overlap은 두 노드가 공유하는 노드의 개수를 두 노드의 이웃 노드의 합집합의 개수로 나눈다. 위 예시 그래프에서 이를 구하면 1/2=0.5가 된다.
RA index (Resource Allocation index)
위의 세 개 measure들은 노드들이 공유하는 이웃 노드를 노드의 degree에 의해 왜곡되지 않도록 normalize했다는 공통점이 있다. 하지만 이를 넘어 노드들이 공유하는 이웃 노드의 중요도를 measure에 반영할 수도 있다. 그 첫번째 예시가 RA index이다. RA index는 다음과 같이 정의한다.

즉, RA index는 두 노드가 서로 공유하는 노드들의 node degree의 역수의 합을 의미한다. 우리의 예시에서는 노드 C만이 서로 공유되기 때문에 이의 degree(4)의 역수인 0.25이 RA index가 된다.
AA index (Adamic-Adar index)
마지막으로, AA index는 RA index와 비슷한 형태를 가지고 있고, 아래와 같이 정의한다.

AA index는 두 노드가 서로 공유하는 노드들의 node degree의 log 값의 역수의 합을 의미한다. 우리의 예시에서는 위에서 보았듯이 노드 C만이 서로 공유되기 때문에 이의 degree(4)의 log의 역수인 1.66이 RA index가 된다.
이번 포스팅에서는 두 노드 사이의 관계를 표현하는 neighborhood overlap, 그 중에서도 local overlap measure에 대해서 알아보았다. 하지만 두 노드 간에 직접적으로 공유하는 이웃인 local neighborhood가 없더라도 두 노드가 서로 관계가 있을 수도 있다. 이를 파악할 수 있는 다양한 지표들에 대해 다음 포스팅에서 알아보겠다.
References
1. Hamilton. William L., Graph Representation Learning.
2. Jure Leskovec. CS224W: Machine Learning with Graphs.








최근댓글