Association Rule의 적용을 위해서는, 각 item들이 각 itemset 안에서 어떤 빈도로 출현했는지, 어떤 item과 함께 나왔는지를 파악하는 것이 필수적이다. 하지만 데이터셋이 큰 경우, 이를 모든 후보 itemset들에 대해 하나하나 검사하는 것은 굉장히 비효율적이다. 이러한 문제를 해결하기 위해 제시된 것이 FP-Growth 알고리즘, Apriori 알고리즘 등이다. 이번 포스팅에서는 이 중 Apriori Algorithm에 대해 알아보겠다.
Motivation
우리가 참치, 방어, 과메기를 함께 사는 사람의 수를 찾고 싶다고 하자. 이때, 이 수는 참치, 방어를 함께 사는 사람의 수보다 클 수 있을까? 절대 그럴 수 없을 것이다. 참치, 방어를 사는 사람 중에서는 과메기가 아닌 광어를 사는 사람도, 대게를 사는 사람도 있을 것이다. 참치, 방어를 사는 사람이 모두 과메기를 산다고 해도 참치, 방어, 과메기를 사는 사람의 수가 참치, 방어를 사는 사람의 수보다 클 수는 없다.
이를 association rule로 적용시켜 보자. 만약 A가 B의 부분집합이라면, A의 support는 B의 support보다 크거나 같을 것이다. 이를 식으로 표현하면 다음과 같다.
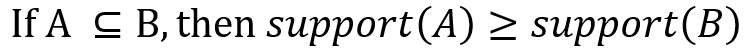
그러므로 B의 support가 우리가 설정해 놓은 minimum support 값보다 크다면, A의 support 또한 minimum support보다 클 것이다. 이를 식으로 표현하면 다음과 같다.

그러므로 만약 우리가 A가 B의 부분집합인 것을 알고 B의 support가 조건을 만족한다는 것을 확인한다면, A의 support도 따라서 조건을 만족할 것이다. Apriori Algorithm은 이 아이디어를 기본으로 한다.
Apriori Algorithm
이제 본격적인 Apriori Algorithm에 대해 설명할 차례이다. 우선, Apriori Algorithm은 이렇게 생겼다. 언제나 알고리즘을 수식으로 보면 무섭다.

하지만 언제나처럼 하나하나 예시와 함께 풀어 설명하도록 하겠다. 다음과 같은 예시 itemset이 있다고 하자. (우리의 minimum support (min_sup) 값은 2/9이다.
| ID | itemset(방문했던 나라) |
| lim | 독일, 스위스, 스페인 |
| song | 스위스, 홍콩 |
| ko | 스위스, 페로 제도 |
| kim | 독일, 스위스, 홍콩 |
| jeong | 독일, 페로 제도 |
| choi | 스위스, 페로 제도 |
| lee | 독일, 페로 제도 |
| jang | 독일, 스위스, 페로 제도, 스페인 |
| park | 독일, 스위스, 페로 제도 |
우선, 하나의 item에 대해 각 item의 빈도를 모두 찾는다. 그것은 다음과 같다. 이를 C_1이라고 한다.
| itemset | count |
| 독일 | 6 |
| 스위스 | 7 |
| 페로 제도 | 6 |
| 홍콩 | 2 |
| 스페인 | 2 |
이제 이들 각각이 minimum support 값을 만족하는지를 살펴 보고, 만족하지 않는 itemset이 있다면 이를 삭제한다. 모두 minimum support(2/9인데, N은 고정이므로 count가 2 이상이면 됨) 값보다 크기 때문에 만족한다. 그러면 모든 조건을 만족하는 itemset은 다음과 같다. 이를 L_1이라고 한다.
| itemset | count |
| 독일 | 6 |
| 스위스 | 7 |
| 페로 제도 | 6 |
| 홍콩 | 2 |
| 스페인 | 2 |
다음으로, 이 L_1에서 다시 C_2를 만들어내기 위해 L_1의 모든 itemset으로 원소가 2개인 집합을 만들고, 그들 각각의 빈도를 구한다. 이때, 각 itemset의 subset의 minimum support가 조건을 만족하지 못했다면 이것이 포함된 것은 모두 제거한다. (위의 motivation을 이용) 우리의 예시에서는 이가 존재하지 않으므로 이는 다음과 같다. 이를 C_2라고 한다.
| itemset | count |
| {독일, 스위스} | 4 |
| {독일, 페로 제도} | 4 |
| {독일, 홍콩} | 1 |
| {독일, 스페인} | 2 |
| {스위스, 페로 제도} | 4 |
| {스위스, 홍콩} | 2 |
| {스위스, 스페인} | 2 |
| {페로 제도, 홍콩} | 0 |
| {페로 제도, 스페인} | 1 |
| {홍콩, 스페인} | 0 |
이제 이들 C_2 중에서 minimum support(2)를 만족하지 못하는 itemset을 없앤다. 위에서 붉게 색칠된 itemset들이 삭제되고, 다음과 같이 L_2가 남는다.
| itemset | count |
| {독일, 스위스} | 4 |
| {독일, 페로 제도} | 4 |
| {독일, 스페인} | 2 |
| {스위스, 페로 제도} | 4 |
| {스위스, 홍콩} | 2 |
| {스위스, 스페인} | 2 |
이제 L_2로부터 C_3를 찾아줄 차례이다. 위에서 한 것과 똑같이 하면 된다. 하지만 이 경우에는 각 itemset의 subset의 minimum support가 조건을 만족하지 못하는 경우가 나온다. 예를 들어, {독일, 스위스, 홍콩}이라는 itemset이 만들어질 수 있는데 (첫 번째 행과 다섯 번째 행), 윗 단계에서 {독일, 홍콩}이 조건을 만족하지 못했기 때문에 이는 C_3에 포함될 수 없다. 이렇게 필요하지 않은 subset을 제거하는 과정을 pruning이라고 한다. 이렇게 C_3를 만들면 다음과 같다.
| itemset | count |
| {독일, 스위스, 페로 제도} | 2 |
| {독일, 스위스, 스페인} | 2 |
이런 식으로 k가 아이템 셋의 전체 숫자가 될 때까지 혹은 L_k가 공집합이 될 때까지 계속 진행하면 된다. 이 과정을 통해 만들어진 L 집합에 속한 모든 itemset들이 minimum support를 만족하는 itemset이 된다.
이번 포스팅에서는 association rule의 적용을 위해 조건을 만족하는 itemset을 찾는 방법 중 하나인 apriori algorithm에 대해 알아보았다. 이를 통해 효율적인 association rule의 활용이 가능할 것이다.
References
Agrawal, Rakesh & Srikant, Ramakrishnan. (2000). Fast Algorithms for Mining Association Rules. Proc. 20th Int. Conf. Very Large Data Bases VLDB. 1215.








최근댓글