KL divergence는 어떤 분포 p, q가 있을 때, 우리는 이들이 얼마나 비슷한 분포인지를 표현하는 measure로, 분포의 entropy와 비교하는 분포 간의 cross entropy 값을 반영한다. 이번 포스팅에서는 확률 분포 사이의 divergence measure 중 하나인 KL divergence(Relative entropy)에 대해 알아보겠다.
정의
분포가 discrete할 때, KL divergence는 아래와 같이 정의할 수 있다.
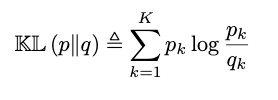
분포가 연속일 때는 KL divergence를 아래와 같이 정의한다.

해석
위의 식이 가지는 의미는 무엇일까? 위 식의 log를 풀어서 써 보면 아래와 같은 식으로 표현할 수 있다.
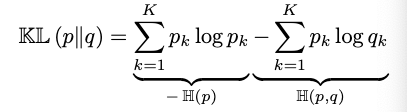
이 식에서 우리는 앞에 있는 plog(p) 값이 p의 entropy를, plog(q) 값이 p와 q의 cross entropy를 표현한다는 것을 알 수 있다. 우리는 entropy를 해당 분포의 복잡도, cross entropy를 p 분포로부터 도출된 데이터를 q로 표현할 때의 복잡도로 해석하기도 한다. 그러므로 우리는 p를 실제 분포, q를 우리가 추정한 분포라고 생각했을 때, 위 식을 실제 분포 p와 비교했을 때 q를 이용해 p로부터 나온 데이터를 표현할 때 얼마나 많은 bit가 추가적으로 사용되어야하는지를 표시한 것이라고 생각할 수 있을 것이다. 즉, 이 값이 낮으면 실제 분포 p와 비슷한 복잡도를 가지기 때문에 p와 비슷한 분포이고, 이 값이 높을수록 추가적으로 많은 bit가 소모되어야 하므로 p와 다른 분포인 것이다.
예시
예를 들어, 두 분포 p, q가 각각 mu_1, mu_2를 평균, sigma_1, sigma_2를 분산으로 가지는 정규분포를 따른다고 하자. 그렇다면 우리는 두 분포의 KL divergence를 아래와 같이 표현할 수 있을 것이다.
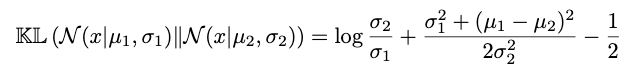
KL divergence와 MLE
우리가 p와 최대한 비슷한 q 분포를 추정하는 것을 목적으로 한다고 하자. 이 말은, 결국 KL divergence를 최소화시키는 q를 찾는 것을 목적으로 하는 것이다. 이를 만족하는 최적의 q를 q*라고 할 때, 우리는 q*를 아래와 같이 표현할 수 있다.

이 때, 위 식에서 p는 주어진 값이기 때문에 결국 우리의 목적은 p(x)log(q(x))의 x에 대한 적분값을 최대화하는 것일 것이다. 우리가 가지고 있는 true distribution인 p 분포를 정확히 표현하기 위해, empirical distribution을 사용하여 표현할 수 있다.

그렇다면 이를 이용하여 우리가 원하는 KL divergence를 최소화시키는 q를 찾기 위해서는 아래와 같은 식을 세울 수 있다.
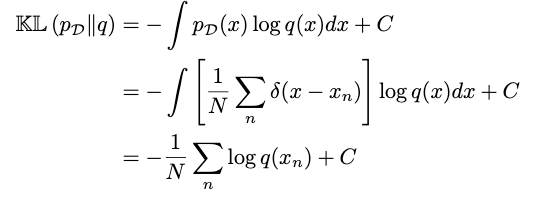
그러므로 위 KL divergence가 최소화되기 위해서는, log(q(x_n))이 최대화되어야 하고, 결국 이는 q의 likelihood를 최대화하는 것이다. 즉, empirical distribution에 대한 KL divergence의 최소화는 likelihood를 최대화하는 것과 같은 의미를 가진다.
이번 포스팅에서는 KL divergence의 정의와 함께 KL divergence를 어떻게 해석해야하는지, 그리고 KL divergence와 MLE의 관계가 무엇인지에 대해 알아보았다. 다음 포스팅에서는 forward KL과 reverse KL에 대해 알아보겠다.
References
1. Probabilistic Machine Learning: An Introduction by Kevin Patrick Murphy. MIT Press, February 2022.








최근댓글