Discrete denoising diffusion probabilistic models (D3PM)은 그래프, 텍스트와 같은 discrete 데이터에 적용할 수 있는 diffusion model을 말한다. D3PM은 Markov transition matrix를 활용해 각각의 diffusion step을 모델링하였고, 이 transition matrix의 선택에 따라 생성 모델의 결과가 달라질 수 있음을 보였다. 이번 글에서는 D3PM 모델이 어떻게 continous가 아닌 discrete 데이터를 모델링하는지에 대해 알아보겠다.
* 이 글은 diffusion model에 대한 기본적인 이해가 있다고 가정한다.
Key idea
우선, D3PM의 핵심 아이디어에 대해 살펴보겠다. D3PM은 위에서도 언급했듯이 Markov transition matrix를 활용하여 diffusion step을 모델링한다. Markov transition matrix를 간단하게 설명하면, 현재의 상태가 어떤 state i로부터 다른 state j로 옮겨갈 확률을 표현한 행렬이다. 그 형태는 아래와 같다.
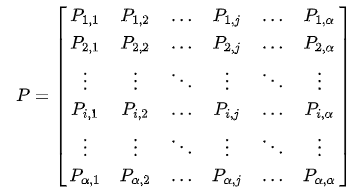
위 행렬에서 (i,j) 성분이 state i로부터 state j로 옮겨갈 확률을 의미한다. 그러므로 Markov transition matrix의 각 row의 합은 1이 될 것이다. 예를 들어, 하나의 전구가 있고 이 전구는 켜지는 것과 꺼지는 것 두 가지의 상태가 있다고 하자. 전구가 켜져있을 때 이것이 꺼질 확률은 1/3, 전구가 꺼져 있을 때 이것이 켜질 확률은 1/4라고 하자. 그러면 이 전구의 상태를 표현하는 transition matrix는 다음과 같은 형태가 될 것이다.
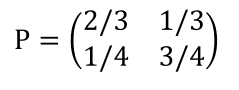
D3PM은 이러한 Markov transition matrix를 identity matrix에 noise를 더하는 형태로 표현한다면, 이것이 noise를 순차적으로 더해가는 diffusion step과 동일하게 작동할 수 있다는 아이디어로부터 시작했다. 즉, 다음과 같이 아주 작은 $\epsilon$을 활용한 형태로 transition matrix를 정의하고, 이를 각 diffusion step마다 데이터를 나타내는 벡터에 곱해주면 이것이 diffusion process가 되는 것이다.

Forward process
Diffusion model의 forward process는 원래 있던 데이터에 noise를 조금씩 더해서 이를 noise 데이터로 만드는 것을 말한다. D3PM의 forward process는 위에서도 언급한 것처럼 transition matrix $Q$로 정의된다. 그러므로 이를 식으로 나타내면 다음과 같다.

이 때, Cat은 categorical distribution을 의미한다. 즉, x 값이 10개의 category가 될 수 있다면, 각 x의 성분은 각 category가 될 확률을 표현하는 것이다. 이전 vector인 $x_{t-1}$에 transition matrix $Q$를 곱함으로써 현재의 vector $x_t$가 도출된다. 이를 활용해서 기존의 diffusion model이 정의하듯이 데이터 $x_0$가 주어졌을 때 $x_t$의 분포를 표현하면 다음과 같다.
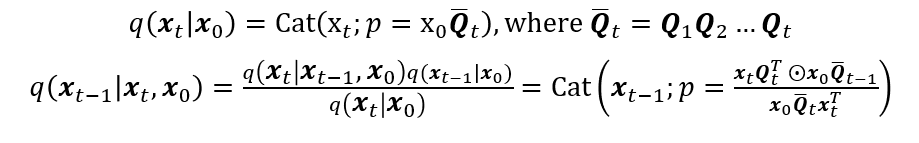
Forward process에서 하나 유의해야할 점은 $\bar{Q_t}$를 stationary distribution을 가지는 transition matrix라고 가정한다는 점이다. Stationary distribution를 가진다는 말은, 간단히 말하면 matrix를 여러 번 곱해도 계속 같은 값을 가지는 벡터를 가지는 행렬을 말한다. 이러한 조건이 있는 이유는 최종 noise인 $x_T$가 하나의 noise vector로 수렴하기를 원하기 때문이다.

Forward process의 transition matrix 선택
D3PM에서 가장 중요한 점은 transition matrix를 어떻게 선택하느냐에 따라 모델의 형태가 완전히 바뀔 수 있다는 점이다. 그러므로 우리는 우리가 원하는 생성된 데이터의 형태가 있다면, transition matrix를 적절하게 선택함으로써 생성 모델의 결과를 바꿀 수 있다.

이러한 transition matrix의 대표적인 예시를 두 개 소개하겠다. 첫 번째는 uniform transition matrix이다. Unfirom transition matrix는 현재 state와 다른 state로 이동하는 모든 확률이 같은 행렬을 말한다. 이는 다음과 같이 정의된다.

두 번째는 absorbing state transition matrix이다. Absorbing state transition matrix는 m이라는 absorbing state가 존재해서, 이 state에 도달하면 다른 state로 더 이상 이동하지 않는다. 이는 다음과 같이 정의된다.

Reverse process
Reverse process는 데이터의 분포 $q(x_0)$를 approximate하는 $p_\theta$를 학습하는 것을 목적으로 한다. Reverse process 또한 transition matrix로 표현되고, 이는 아래 식과 같다.
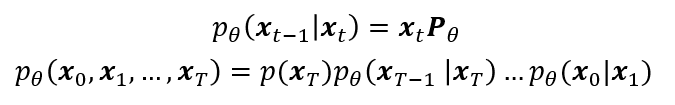
이러한 reverse process에 대한 marginalization을 활용해서 우리가 원하는 $p_\theta(x_0)$를 구할 수 있다.
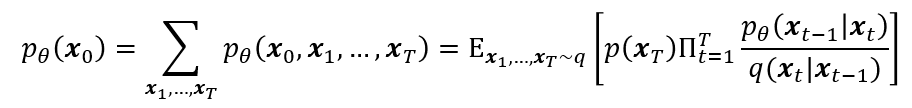
이를 통해서 얻을 수 있는 $q(x_0)$와 $p_\theta(x_0)$ 사이의 KL divergence를 D3PM의 loss function으로 정의한다. 이는 다음과 같은 variational lower bound 형태로 표현할 수 있다.

Experiments
이렇게 정의한 forward process와 reverse process로부터 generative model을 구성해서, 적절한 transition matrix를 선택하여 이들로부터 데이터를 만들어내면 다음과 같은 좋은 결과를 얻을 수 있다.


이번 글에서 우리는 diffusion model을 discrete 데이터에 적용할 수 있게 하는 모델인 D3PM에 대해 알아보았다. 그래프, text와 같은 discrete 데이터에 대해서는 D3PM으로 생성한 데이터가 더 좋은 성능을 보여줄 수도 있을 것이다.
References
Austin, J., Johnson, D. D., Ho, J., Tarlow, D., & van den Berg, R. (2021). Structured denoising diffusion models in discrete state-spaces. Advances in Neural Information Processing Systems, 34, 17981-17993.








최근댓글