Denoising diffusion probabilistic models (DDPM)은 diffusion model을 활용한 image generative model을 제시한 논문으로, 기존의 diffusion model의 loss term과 parameter estimation 과정을 더 학습이 잘 되는 방향으로 발전시킨 논문이다. 이번 글에서는 DDPM 모델이 어떻게 작동하는지에 대해서 알아보겠다.
* 이 글은 diffusion model에 대한 이해가 있다고 가정한다.
시작하기 전에 간단히 diffusion model을 복습하자면, diffusion model은 기본적으로 data로부터 noise를 만들어내는 forward (diffusion) process $q(x_{1:T}|x_0)$와 noise로부터 data를 만들어내는 reverse process $p(x_{0:T})$로 이루어져 있다. Diffusion model은 다른 generative model들처럼 true data distribution $p_\theta(x_0)$를 학습하는 것을 목표로 하고, 이는 다음 loss를 minimize하면서 진행된다.

위 loss를 minimze하면서 reverse process를 학습하여 noise로부터 data를 만들어내는 generative model을 만들어낸다. 위 loss는 다음과 같이 normal distribution 사이의 KL divergence 형태로도 표현될 수 있다.
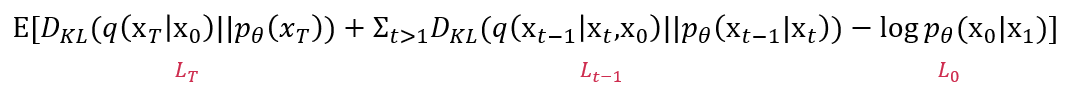
그럼 이를 바탕으로 해서 DDPM은 어떻게 모델링을 진행하는지 알아보겠다.
Forward process
DDPM의 forward process는 기본적인 diffusion model과 똑같이 data에 Gaussian noise를 더하는 형태로 정의된다. 이 때, $\beta_t$는 학습을 할 수도 있고, 어떤 함수로 정의할 수도 있지만 DDPM에서는 미리 정해진 상수로 정의한다. 그러므로 forward process에서는 별도의 학습이 필요하지 않다.
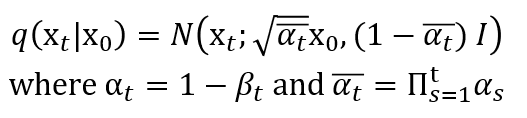
Reverse process
DDPM의 reverse process에서 우리는 다음 식에서의 $\mu_\theta$와 $\Sigma_\theta$를 학습해야 한다.

우리는 위에서 언급했듯이 다음과 같은 loss function을 최소화하는 것을 목적으로 한다.
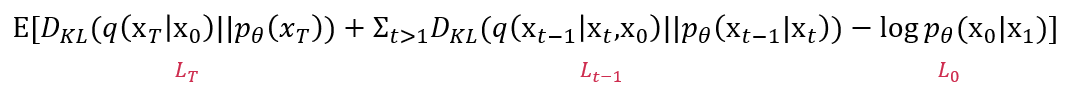
이 각각의 loss function을 DDPM에서 어떻게 최소화하는지를 알면, 우리가 어떻게 parameter를 학습해야할지도 알 수 있을 것이다. 이들 각각을 하나씩 살펴보겠다.
$L_T$
$L_T$에서 우리는 $q$와 $p(x_T)$를 각각 학습이 필요하지 않은 파라미터를 가지는 정규분포로 가정했기 때문에, 이를 최소화하기 위해서 우리가 학습해야하는 파라미터는 없다. 그러므로 학습하는 동안 이 loss는 무시가 가능하다.
$L_{t-1}$
$L_{t-1}$에서 우리는 이를 계산하기 위해서 첫 번째로 $q(x_{t-1}|x_t,x_0)$의 분포를 알아내고, 두 번째로 $p_\theta(x_{t-1}|x_t)$를 알아내기 위해 $\Sigma_\theta$와 $\mu_\theta$를 알아내야 한다. 이를 순서대로 하나씩 살펴보겠다.
1. $q(x_{t-1}|x_t,x_0)$
이는 우리가 기존 diffusion model에서 알아보았던 것처럼 다음과 같은 형태로 정의할 수 있다. (증명은 diffusion model 글을 참고한다.)

2. $p_\theta(x_{t-1}|x_t)$
$\Sigma_\theta$
p의 표준편차는 $\sigma_t^2I$라는 상수 행렬로 정의한다. 그러므로 이에 대해서는 학습이 필요하지 않다.
$\mu_\theta$
마지막으로, p의 평균은 다음과 같이 정의한다.
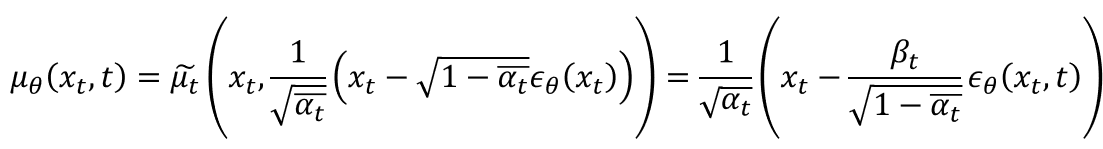
이는 다음과 같은 과정을 통해 증명할 수 있다. (증명은 생략해도 좋다.)
첫 번째 =은 forward process가 다음과 같은 형태이기 때문에, 우리가 $x_t(x_0,\epsilon)=\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon$이라고 쓸 수 있고, 이를 이용해서 $x_0$를 표현하면 위 식과 동일해지기 때문이다.

다음으로, 두 번째 =은 그 증명 과정이 조금 복잡하다. 우선, 우리는 다음과 같은 사실들을 알고 있다.

이들을 활용해서 식을 전개해보면 다음과 같다.

이렇게 위 과정을 통해서 $\mu_\theta$를 얻어내면, 이를 활용해서 우리는 $p_\theta(x_{t-1}|x_t)$로부터 $x_{t-1}$을 샘플링할 수 있다. 이 과정은 다음과 같은 알고리즘으로 표현할 수 있다.

또한 우리는 이렇게 얻어낸 파라미터들을 활용해 loss function을 다음과 같이 normal distribution 간의 KL divergence를 계산한 식으로 표현할 수 있다.
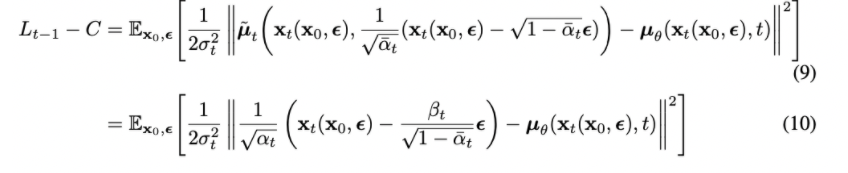
그리고 마지막으로, 우리는 위의 loss function을 epsilon에 대한 식의 형태로 다시 한 번 표현할 수 있다. 이를 simplified objective function이라고 부르고, 이러한 loss function을 통해 training을 하면 학습이 좀 더 잘 된다는 것을 확인할 수 있다.
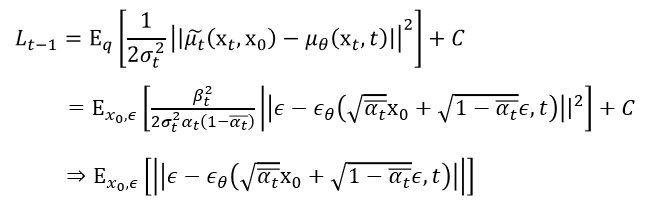
결론적으로, DDPM의 training 과정을 몇 줄의 알고리즘으로 요약하면, 다음과 같다.

$L_0$
마지막으로, loss function의 마지막 구성 요소인 $L_0$에 대해 알아보겠다. 이는 그냥 간단한 두 normal 분포 사이의 KL divergence이기 때문에 다음과 같은 간단한 형태로 표현할 수 있다.

Experiments
사실상 DDPM 논문의 핵심은 reverse process의 $L_{t-1}$을 예쁜 형태로 다시 정의한 것에 있다. 이렇게 forward process와 reward process를 정의하여 generative model을 구성하고, 이들로부터 사진 데이터를 만들어보면, 다음과 같이 좋은 퀄리티의 사진들을 만들어냄을 알 수 있다.

이번 글에서 우리는 가장 간단한 형태의 diffusion model에 이어 DDPM이 무엇인지에 대해 증명과 함께 알아보았다. Diffusion model 논문들은 수식이 굉장히 복잡해서 이해하기가 쉽지 않은데, 공부하다보면 비슷한 flow로 논문들이 전개되고 있음을 알 수 있다. 다음 글에서는 discrete 데이터에 적절한 diffusion model을 제시한 D3PM과 any-order autoregressive model과 diffusion model을 엮어낸 autoregressive diffusion model 등에 대해서도 알아보겠다.
약속이 없으면 고대로 야근 때리는 바쁜 평일을 보내고 있어서 글 쓰기가 쉽지 않았는데 주말에 화이팅해보겠다.. 올해에 200번째 글 채우기 프로젝트 화이팅
References
Ho, J., Jain, A., & Abbeel, P. (2020). Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems, 33, 6840-6851.








최근댓글